
分析 求出曲线的普通方程为x2=4y,从而求出曲线的焦点F(0,1),由此利用两点间距离公式能求出|AF|的值.
解答 解:∵曲线$\left\{\begin{array}{l}{x=2\sqrt{2}cosθ}\\{y=1+cos2θ}\end{array}\right.$(θ∈R),
∴y=1+2cos2θ-1=2cos2θ,
又x2=8cos2θ,
∴曲线的普通方程为x2=4y,
∴曲线的焦点F(0,1),
∵A(1,0),∴|AF|=$\sqrt{1+1}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查线段长的求法,考查极坐标方程、直角坐标方程、参数方程的互化、两点间距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{17\sqrt{2}}{26}$ | B. | -$\frac{7\sqrt{2}}{26}$ | C. | $\frac{7\sqrt{2}}{26}$ | D. | $\frac{17\sqrt{2}}{26}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
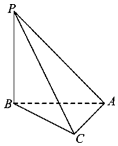 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=2CA=2,则三棱锥P-ABC的外接球表面积为( )| A. | 3π | B. | 5π | C. | 12π | D. | 20π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $d≈\root{3}{{\frac{60}{31}V}}$ | B. | $d≈\root{3}{2V}$ | C. | $d≈\root{3}{{\frac{15}{8}V}}$ | D. | $d≈\root{3}{{\frac{21}{11}V}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com