
分析 (1)为古典概型,可得总数为4×4=16种,符合题意得为4种,代入古典概型得公式可得;
(2)为几何概型,设甲到达时刻为x,乙到达时刻为y,可得0≤x≤60,0≤y≤60,作出图象由几何概型的公式可得
解答 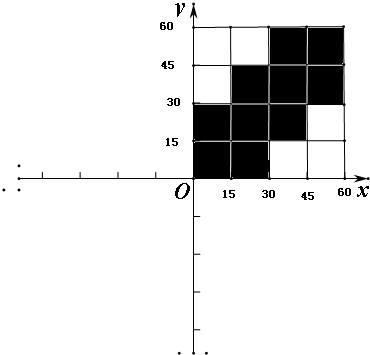 解:(1)他们乘车总的可能结果数为4×4=16种,
解:(1)他们乘车总的可能结果数为4×4=16种,
乘同一班车的可能结果数为4种,
由古典概型知甲乙乘同一班车的概率为P=$\frac{1}{4}$;
(2)设甲到达时刻为x,乙到达时刻为y,可得0≤x≤60,0≤y≤60,记事件B表示“最多等一辆,且两人同乘一辆车”,
则:B={(x,y)|0≤x≤15,0≤y≤30;15<x≤30,0≤y≤45;30<x≤45,15≤y≤60;45<x≤60,30<y≤60;},如图
概率为P(B)=$\frac{15×30+15×45+15×45+15×30}{60×60}$=$\frac{5}{8}$.
点评 本题考查几何概型的求解,涉及古典概型,准确作出图象是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
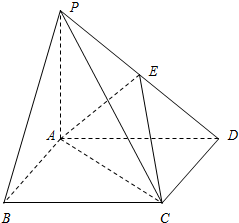 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com