
分析 (1)先求出集合A,根据二次根式的性质求出集合B、C即可;(2)若A∪C=C,则A⊆C,得到关于a的不等式,解出即可.
解答 解:(1)由-(x-2a)(x-a)>0得(x-2a)(x-a)<0,又因为a>0,且a≠1
所以a<x<2a,所以A=(a,2a)…(2分)
对于函数$f(x)=\sqrt{9-{3^x}}$,由9-3x≥0得x≤2,B=[2,+∞)…(4分)
所以0<3x≤9,0≤9-3x<9,所以$f(x)=\sqrt{9-{3^x}}∈[{0,3})$,C=[0,3)…(6分)
(2)若A∪C=C,则A⊆C,
则有$\left\{{\begin{array}{l}{a>0}\\{a≠1}\\{2a≤3}\end{array}}\right.$⇒$0<a≤\frac{3}{2}$且a≠1,
所以实数a的取值范围是$0<a≤\frac{3}{2}$且a≠1.…(12分)
点评 本题考查了函数的定义域问题,考查集合的包含关系,考查二次根式以及对数函数的性质,是一道中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 挂果个数区间 | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
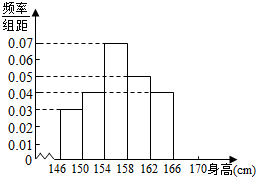 为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:
为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:| 组 别 | 频数 | 频率 |
| [146,150) | 6 | 0.12 |
| [150,154) | 8 | 0.16 |
| [154,158) | 14 | 0.28 |
| [158,162) | 10 | 0.20 |
| [162,166) | 8 | 0.16 |
| [166,170) | m | n |
| 合 计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com