
 Ϊ���˽�ijУ��һŮ������������������ȡM����һŮ���������ߣ����������������г�Ƶ�ʷֲ������
Ϊ���˽�ijУ��һŮ������������������ȡM����һŮ���������ߣ����������������г�Ƶ�ʷֲ������| �顡�� | Ƶ�� | Ƶ�� |
| [146��150�� | 6 | 0.12 |
| [150��154�� | 8 | 0.16 |
| [154��158�� | 14 | 0.28 |
| [158��162�� | 10 | 0.20 |
| [162��166�� | 8 | 0.16 |
| [166��170�� | m | n |
| �ϡ��� | M | 1 |
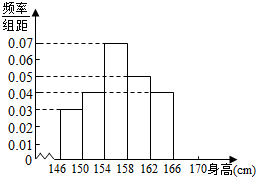
���� ����Ƶ�ʷֲ�ֱ��ͼ�У�С���εĸߵ���ÿһ���$\frac{Ƶ��}{���}$��������Ƶ�������ȣ�С���ε����������һ���Ƶ�ʣ���������Ƶ�ʳ��Ըߣ�������ϵ���ɽ�ã�
���������ɣ�
��������λ��Ϊx����154��x��158�����ö��弴�������
���  �⣺����������M=$\frac{8}{0.16}$=50����������[166��170��������Ƶ����Ϊm=50-��8+6+14+10+8��=4��
�⣺����������M=$\frac{8}{0.16}$=50����������[166��170��������Ƶ����Ϊm=50-��8+6+14+10+8��=4��
Ƶ��Ϊn=$\frac{4}{50}$=0.08��
����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
��������λ��Ϊx����154��x��158��
��0.12+0.16+0.07��x-154��=0.08+0.16+0.20+0.07��158-x����
���x��157.14��
���������λ��Ϊ157.14cm��
���� ������Ҫ����Ƶ�ʷֲ�ֱ��ͼ�ͱ���������ͬѧ��ͨ����֪��������Ƶ��ֱ��ͼ���������������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | -$\frac{1}{4}$ | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com