
分析 (1)根据数量积的计算公式即可求出$\overrightarrow{a}•\overrightarrow{b}$,而由$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$即可求出$|\overrightarrow{a}+\overrightarrow{b}|$;
(2)同理可以求出$|\overrightarrow{a}-\overrightarrow{b}|$的值,而可求出$(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}=-3$,从而根据向量夹角余弦的计算公式即可求出cosθ.
解答 解:(1)$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°$=$1×2×(-\frac{1}{2})=-1$;
∴$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={1}^{2}+2×(-1)+{2}^{2}=3$;
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{3}$;
(2)同理可求得$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{7}$;
$(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}={1}^{2}-{2}^{2}=-3$;
∴$cosθ=\frac{(\overrightarrow{a}+\overrightarrow{b})•(\overrightarrow{a}-\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}||\overrightarrow{a}-\overrightarrow{b}|}=\frac{-3}{\sqrt{3}•\sqrt{7}}$=$-\frac{\sqrt{21}}{7}$.
点评 考查向量数量积的运算及其计算公式,根据$|\overrightarrow{a}+\overrightarrow{b}{|}^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}$求$|\overrightarrow{a}+\overrightarrow{b}|$的方法,以及向量夹角余弦的计算公式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 挂果个数区间 | [155,165) | [165,175) | [175,185) | [185,195] |
| 频数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
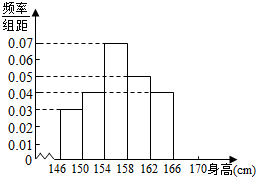 为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:
为了了解某校高一女生的身高情况,随机抽取M个高一女生测量身高,所得数据整理后列出频率分布如表:| 组 别 | 频数 | 频率 |
| [146,150) | 6 | 0.12 |
| [150,154) | 8 | 0.16 |
| [154,158) | 14 | 0.28 |
| [158,162) | 10 | 0.20 |
| [162,166) | 8 | 0.16 |
| [166,170) | m | n |
| 合 计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
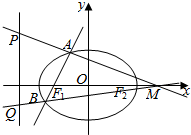 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-1,0),离心率是e,点(1,e)在椭圆上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com