练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．如图，矩形ABCD中，AB=2，BC=4，以矩形ABCD的中心为原点，过矩形ABCD的中心平行于BC的直线为x轴，建立直角坐标系，
    （1）求到直线AD、BC的距离之积为1的动点P的轨迹；
    （2）若动点P分别到线段AB、CD中点M、N的距离之积为4，求动点P的轨迹方程，并指出曲线的性质（对称性、顶点、范围）；
    （3）已知平面上的曲线C及点P，在C上任取一点Q，线段PQ长度的最小值称为点P到曲线C的距离．若动点P到线段AB的距离与射线CD的距离之积为4，求动点P的轨迹方程，并作出动点P的大致轨迹．

    分析 （1）利用到直线AD、BC的距离之积为1，建立方程，即可求出动点P的轨迹；
    （2）$\sqrt{（x+2）^{2}+{y}^{2}}$•$\sqrt{（x-2）^{2}+{y}^{2}}$=4，化简可得结论；
    （3）同时从几何和代数角度进行分析，即可得出结论．

    解答 解：（1）设P（x，y），则|y-1||y+1|=1…2分
    化简得y=±$\sqrt{2}$或y=0．
    故动点P的轨迹为三条平行线；…4分
    （2）$\sqrt{（x+2）^{2}+{y}^{2}}$•$\sqrt{（x-2）^{2}+{y}^{2}}$=4，
    化简得 $（\sqrt{{x}^{2}+1}-2）^{2}+{y}^{2}=1$
    对称性：关于原点、x、y轴对称；…6分
    顶点：（2$\sqrt{2}$，0），（-2$\sqrt{2}$，0），（0，0）；…8分
    范围：|x|≤2$\sqrt{2}$，|y|≤1…10分
    （3）同时从几何和代数角度进行分析
    当y＜-1时，y=-1-$\sqrt{4\sqrt{{x}^{2}+1}-{x}^{2}-4}$，…12分
    当-1≤y≤1时，x=±2$\sqrt{2}$或x=0，…14分
    当y＞1时，y=1+$\sqrt{\frac{16}{（x-2）^{2}}-（x+2）^{2}}$，…16分
    作轨迹大致如图．分三个区域给分：
    ①在直线y=-1的下方：两段曲线；
    ②在两直线y=-1，y=1之间：三条平行线；
    ③在直线y=1的上方：三条曲线．…18分．

    点评 本题考查轨迹方程，考查学生的计算能力，确定轨迹方程是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

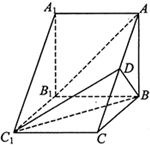    17．在三棱柱ABC-A1B1C1中，侧棱BB1⊥底面A1B1C1，D为AC 的中点，A1B1=BB1=2，A1C1=BC1，∠A1C1B=60°．
    （Ⅰ）求证：AB1∥平面BDC1；
    （Ⅱ）求多面体A1B1C1DBA的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知函数f（x）=-1+5（x-1）-C${\;}_{5}^{2}$（x-1）2+C${\;}_{5}^{3}$（x-1）3-5（x-1）4+（x-1）5，若f（a）=32，则实数a的值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设函数fn（x）=xn+ax+b（n∈N*，a，b∈R）．
    （1）设n≥2，a=1，b=-1，证明：fn（x）在区间（$\frac{1}{2}$，1）内存在唯一的零点．
    （2）设n=2，若对任意x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤4，求a的取值范围．
    （3）在（1）条件下，设fn（x）在（$\frac{1}{2}$，1）内零点，试说明数列x2，x3，…，xn的增减性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在极坐标系中，动点M从M0（1，0）出发，沿极轴ox方向作匀速直线运动，速度为3米/秒，同时极轴ox绕极点o按逆时针方向作等角速度旋转，角速度为2米/秒．则动点M的极坐标方程ρ=1+$\frac{3}{2}$θ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．如图，边长为2的正方形ABCD所在平面与圆O所在平面相交于CD，CE为圆O的直径，线段CD为圆O的弦，AE垂直于圆O所在平面，且AE=1
    （1）求异面直线CB与DE所成角的大小；
    （2）将△ACD（及其内部）绕AE所在直线旋转一周形成一几何体，求该几何体体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．对于函数f（x）=x3cos3（x+$\frac{π}{6}$），下列说法正确的是（　　）
    A．f（x）是奇函数且在（-$\frac{π}{6}$，$\frac{π}{6}$）上递增B．f（x）是奇函数且在（-$\frac{π}{6}$，$\frac{π}{6}$）上递减
    C．f（x）是偶函数且在（0，$\frac{π}{6}$）上递增D．f（x）是偶函数且在（0，$\frac{π}{6}$）上递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．将函数y=sinx-$\sqrt{3}$cosx的图象沿x轴向右平移a个单位（a＞0），所得图象关于y轴对称，则a的最小值为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{2}$C．$\frac{7π}{6}$D．$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知：a?α，b?α，且a∥b，求证：a∥α

    查看答案和解析>>

    同步练习册答案