Question

18．已知点O是△ABC内一点，$\overrightarrow{OA}$+2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=0．
（1）△AOB与△AOC的面积之比为$\frac{3}{2}$；
（2）△ABC与△AOC的面积之比为3；
（3）△ABC与四边形ABOC的面积之比为$\frac{6}{5}$．

Answer 1

分析 通过作辅助线如图，利用三角形的面积计算公式及比例关系，得到S_△AOB：S_△AOC：S_△BOC=3：2：1，计算即可．

解答 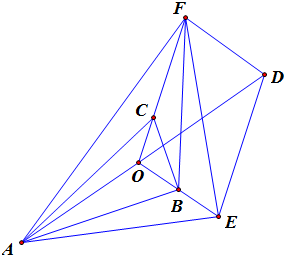解：如图，延长AO至D使得AO=DO，延长OB至E使得OE=2OB，
延长OC至F使得OF=3OC，连结AF、FD、AE、ED、EF、BF，
∵2$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{OD}$，
∴四边形OEDF是平行四边形，
∴S_△AOB=$\frac{1}{2}$S_△AOE=$\frac{1}{2}$S_△EOD，
S_△AOC=$\frac{1}{3}$S_△AOF=$\frac{1}{3}$S_△ODF，
S_△BOC=$\frac{1}{3}$S_△BOF=$\frac{1}{2}$•$\frac{1}{3}$S_△OEF，
又∵S_△EOD=S_△ODF=S_△OEF，
∴S_△AOB：S_△AOC：S_△BOC=3：2：1，
∴$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=$\frac{3}{2}$，$\frac{{S}_{△ABC}}{{S}_{△AOC}}$=$\frac{3+2+1}{2}$=3，$\frac{{S}_{△ABC}}{{S}_{四边形ABOC}}$=$\frac{3+2+1}{3+2}$=$\frac{6}{5}$，
故答案为：$\frac{3}{2}$，3，$\frac{6}{5}$．

点评 本题以三角形面积公式为载体，考查向量模的知识，注意解题方法的积累，属于中档题．