
分析 (Ⅰ)记Ai表示事件:第i局甲获胜,i=3,4,5,Bj表示事件:第j局乙获胜,j=3,4.记B表示事件:甲获得这次比赛的胜利.因前两局中,甲、乙各胜一局,故甲获得这次比赛的胜利当且仅当在后面的比赛中,甲先胜2局,从而B=A3•A4+B3•A4•A5+A3•B4•A5,由于各局比赛结果相互独立,由此能求出甲获得这次比赛胜利的概率.
(Ⅱ)经过5局比赛,甲获胜的概率为P(B3•A4•A5)+P(A3•B4•A5);经过5局比赛,乙获胜的概率为P(A3•B4•B5)+P(B3•A4•B5),由此能求出经过5局比赛,比赛结束的概率.
解答 解:(Ⅰ)记Ai表示事件:第i局甲获胜,i=3,4,5,Bj表示事件:第j局乙获胜,j=3,4.
记B表示事件:甲获得这次比赛的胜利.
因前两局中,甲、乙各胜一局,故甲获得这次比赛的胜利当且仅当在后面的比赛中,甲先胜2局,
从而B=A3•A4+B3•A4•A5+A3•B4•A5,
由于各局比赛结果相互独立,
故P(B)=P(A3•A4)+P(B3•A4•A5)+P(A3•B4•A5)
=P(A3)P(A4)+P(B3)P(A4)P(A5)+P(A3)P(B4)P(A5)
=0.6×0.6+0.4×0.6×0.6+0.6×0.4×0.6=0.648.
(Ⅱ)经过5局比赛,甲获胜的概率为
P(B3•A4•A5)+P(A3•B4•A5)=0.4×0.6×0.6+0.6×0.4×0.6=0.288;
经过5局比赛,乙获胜的概率为
P(A3•B4•B5)+P(B3•A4•B5)=0.6×0.4×0.4+0.4×0.6×0.4=0.192.
所以经过5局比赛,比赛结束的概率为0.288+0.192=0.48.
点评 本题考查互斥事件有一个发生的概率、相互独立事件同时发生的概率,解题之前,要分析明确事件间的关系,一般先按互斥事件分情况,再由相互独立事件的概率公式,进行计算.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3π}{16}$ | D. | $\frac{12+3π}{32}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
某商店销售10台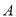 型和20台
型和20台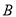 型电脑的利润为4000元,销售20台
型电脑的利润为4000元,销售20台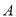 型和10台
型和10台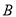 型电脑的利润为3500元.
型电脑的利润为3500元.
(1)求每台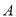 型电脑和
型电脑和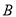 型电脑的销售利润;
型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中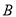 型电脑的进货量不超过A型电脑的2倍.设购进
型电脑的进货量不超过A型电脑的2倍.设购进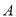 掀电脑
掀电脑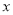 台,这100台电脑的销售总利润为
台,这100台电脑的销售总利润为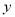 元.
元.
①求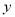 与
与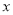 的关系式;
的关系式;
②该商店购进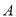 型、
型、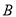 型各多少台,才能使销售利润最大?
型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对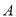 型电脑出厂价下调
型电脑出厂价下调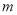 (
(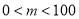 )元,且限定商店最多购进
)元,且限定商店最多购进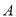 型电脑70台.若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案.
型电脑70台.若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com