
分析 x>0,y>0,(x+$\frac{4}{y}$)2+$\frac{y}{x}$=${x}^{2}+\frac{16}{{y}^{2}}$+$\frac{8x}{y}$+$\frac{y}{x}$≥$\frac{8x}{y}$+8xy+$\frac{y}{x}$=$\frac{16x}{y}$+$\frac{x}{y}$≥8,即可得出结论.
解答 解:∵x>0,y>0,
∴(x+$\frac{4}{y}$)2+$\frac{y}{x}$=${x}^{2}+\frac{16}{{y}^{2}}$+$\frac{8x}{y}$+$\frac{y}{x}$≥$\frac{8x}{y}$+8xy+$\frac{y}{x}$=$\frac{16x}{y}$+$\frac{x}{y}$≥8,
当且仅当$\left\{\begin{array}{l}{{x}^{2}=\frac{16}{{y}^{2}}}\\{\frac{16x}{y}=\frac{x}{y}}\end{array}\right.$,即x=1,y=4时,(x+$\frac{4}{y}$)2+$\frac{y}{x}$的最小值为8,
故答案为:8.
点评 本题考查函数的最值,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题

| A. | 2 | B. | 4 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{13}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
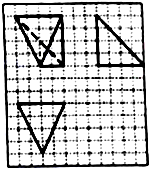
| A. | 32 | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+3i | B. | 4-3i | C. | -4+3i | D. | -4-3i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.
如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com