如图.直角梯形ABCD绕底边AD所在直线EF旋转.在旋转前.非直角的腰的端点A可以在DE上选定．当点A选在射线DE上的不同位置时.形成的几何体大小.形状不同.分别画出它的三视图并比较其异同点．题目和参考答案——青夏教育精英家教网—

20．

如图，直角梯形ABCD绕底边AD所在直线EF旋转，在旋转前，非直角的腰的端点A可以在DE上选定．当点A选在射线DE上的不同位置时，形成的几何体大小、形状不同，分别画出它的三视图并比较其异同点．

分析对点A选在射线DE上的不同位置分别讨论，看旋转后的几何体可由哪些简单几何体构成，再画出几何体的三视图．

解答解：（1）当点A在图射线DE的位置时，绕EF旋转一周所得几何体为底面半径为CD的圆柱和圆锥拼成，
其三视图如图；

（2）当点A在图中射线DE的位置，即B到EF所作垂线的垂足时，旋转后几何体为圆柱，
其三视图如图；

（3）当点A位于如图所示位置时，其旋转所得几何体为圆柱中挖去同底的圆锥，
其三视图如图；

（4）当点A位于点D时，如图，其旋转体为圆柱中挖去一个同底等高的圆锥，
其三视图如图；

点评本题主要考查了空间几何体三视图的应用问题，也考查了旋转体的应用问题，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

10．设x＞0，y＞0，则（x+$\frac{4}{y}$）²+$\frac{y}{x}$的最小值为8．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．已知函数f（x）=2lnx-$\frac{1}{2}$ax²-bx-1．
（1）当a=b=1时，求函数f（x）的最大值；
（2）当b=1，a≥0时，求函数f（x）的单调区间；
（3）当a=0，b=-4时，方程2m=$\frac{f（x）}{{x}^{2}}$有唯一实数根，求正实数m的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．已知a＜0，函数$f（x）=acosx+\sqrt{1+sinx}+\sqrt{1-sinx}$，其中$x∈[{-\frac{π}{2}\;，\;\;\frac{π}{2}}]$．
（1）设$t=\sqrt{1+sinx}+\sqrt{1-sinx}$，求t的取值范围，并把f（x）表示为t的函数g（t）；
（2）求函数f（x）的最大值（可以用a表示）；
（3）设a=-1，若对区间$[{-\frac{π}{2}\;，\;\;\frac{π}{2}}]$内的任意x₁，x₂，若有|f（x₁）-f（x₂）|≤m，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．如图1所示，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，EF∩AC=O，沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图2所示五棱锥P-ABFED，且AP=$\sqrt{30}$，

（1）求证：BD⊥平面POA；
（2）求二面角B-AP-O的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．准线方程为y=4的抛物线的标准方程是（　　）

A．

x²=16y

B．

x²=8y

C．

x²=-16y

D．

x²=-8y

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．函数y=f（x）是定义在R上的偶函数，当x≥0时，f（x）=x²-2x-1．
（1）求f（x）的函数解析式；
（2）写出函数f（x）的单调区间及最值；
（3）当关于x的方程f（x）=m有四个不同的解时，求m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．

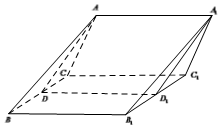如图三棱柱ABC-A₁B₁C₁，AB=BC=CA，D，D₁分别是BC，B₁C₁的中点，四边形ADD₁A₁是菱形，且平面ADD₁A₁⊥平面CBB₁C₁．
（Ⅰ）求证：四边形CBB₁C₁为矩形；
（Ⅱ）若$∠AD{D_1}=\frac{π}{3}$，且A-BB₁C₁C体积为$\sqrt{3}$，求三棱柱ABC-A₁B₁C₁的侧面积．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

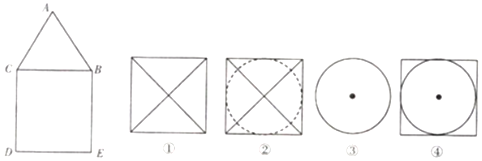
10．已知某组合体的正视图与侧视图相同，如图所示，其中AB=AC，四边形BCDE为矩形，则该组合体的俯视图可以是①②③④（把你认为正确的图的序号都填上）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学