练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知某组合体的正视图与侧视图相同，如图所示，其中AB=AC，四边形BCDE为矩形，则该组合体的俯视图可以是①②③④（把你认为正确的图的序号都填上）

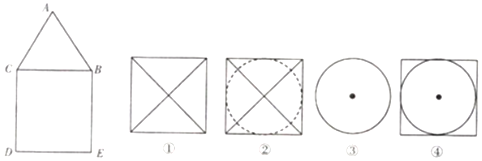
    分析 根据几何体的正视图与侧视图相同，得出组合体可以是正四棱柱与正四棱锥的组合体，
    也可以是圆柱与正四棱锥的组合体，也可以是圆柱与圆锥的组合体，
    也可以是正四棱柱与圆锥的组合体，分四种情况得出对应俯视图．

    解答 解：由组合体的正视图与侧视图可知，
    该组合体可以是正四棱柱与正四棱锥的组合体，则该组合体的俯视图为①；
    该组合体可以是圆柱与正四棱锥的组合体，则该组合体的俯视图为②；
    该组合体可以是圆柱与圆锥的组合体，则该组合体的俯视图为③；
    该组合体可以是正四棱柱与圆锥的组合体，则该组合体的俯视图为④．
    故答案为：①②③④．

    点评 本题主要考查了空间组合体的三视图画法问题，也考查了识图能力与空间想象能力，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．如图，直角梯形ABCD绕底边AD所在直线EF旋转，在旋转前，非直角的腰的端点A可以在DE上选定．当点A选在射线DE上的不同位置时，形成的几何体大小、形状不同，分别画出它的三视图并比较其异同点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设定义域为R的函数f（x）=$\left\{\begin{array}{l}{0}&{x=1}\\{|lg|x-1||}&{x≠1}\end{array}\right.$，则关于x的方程f2（x）+bf（x）+c=0有7个不同实数解的充要条件是（　　）
    A．b＜0且c＞0B．b＞0且c＜0C．b＜0且c=0D．b＞0且c=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若两个球的体积之比为1：8，则这两个球的表面积之比为（　　）
    A．1：2B．1：4C．1：8D．1：16

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设M是△ABC边BC上的任意一点，$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{NM}$，若$\overrightarrow{AN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$，则λ+μ=（　　）
    A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=（2-a）（x-1）-2lnx，a∈R．
    （Ⅰ）若a=1，求曲线y=f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）若不等式f（x）＞0在区间（0，$\frac{1}{2}$）上恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

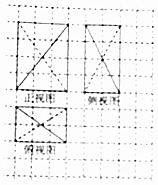    2．如图，网格纸上小正方形的边长为1，粗线（实线和虚线）为某几何体的三视图，则该几何体外接球的表面积为（　　）
    A．24πB．29πC．48πD．58π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知a=sin$\frac{2π}{7}$，b=cos$\frac{2π}{7}$，c=tan$\frac{2π}{7}$，则（　　）
    A．b＜a＜cB．c＜b＜aC．b＜c＜aD．a＜b＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知实数x，y满足$\left\{\begin{array}{l}{y≥x+2}\\{x+y≤6}\\{x≥1}\end{array}\right.$，则z=2|x-2|+|y|的最小值是（　　）
    A．6B．5C．4D．3

    查看答案和解析>>

    同步练习册答案