
分析 (1)当x<0时,-x>0,由已知中当x≥0时,f(x)=x2-2x-1,及函数f(x)是定义在R上的偶函数,可求出当x<0时函数的解析式,进而得到答案,
(2)由二次函数的图象画法可得到函数的草图;根据图象写出函数f(x)的单调区间及最值;
(3)由图象可得结论.
解答 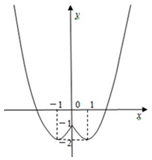 解:(1)当x<0时,-x>0,
解:(1)当x<0时,-x>0,
则当x≥0时,f(x)=x2-2x-1,
则f(-x)=(-x)2-2(-x)-1=x2+2x-1,
∵f(x)是偶函数,∴f(-x)=f(x)=x2+2x-1,
∴$f(x)=\left\{{\begin{array}{l}{{x^2}-2x-1,x≥0}\\{{x^2}+2x-1,x<0}\end{array}}\right.$;
(2)单调增区间为[-1,0]和(1,+∞),单调减区间为(-∞,-1]和[0,1];
当x=1或x=-1时,f(x)有最小值-2,无最大值;
(3)关于x的方程f(x)=m有四个不同的解,即有直线y=m与y=f(x)的图象有四个交点,由图象可知,m的取值范围是(-2,-1).
点评 本题考查的知识点是函数图象,函数的单调区间,函数的值域,是函数图象和性质的综合应用,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{32}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1365石 | B. | 338石 | C. | 169石 | D. | 134石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
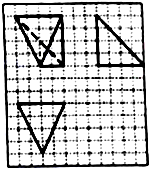
 如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.
如图,直角梯形ABCD绕底边AD所在直线EF旋转,在旋转前,非直角的腰的端点A可以在DE上选定.当点A选在射线DE上的不同位置时,形成的几何体大小、形状不同,分别画出它的三视图并比较其异同点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{24}$ | B. | $\frac{5π}{48}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<0且c>0 | B. | b>0且c<0 | C. | b<0且c=0 | D. | b>0且c=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
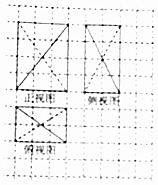 如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗线(实线和虚线)为某几何体的三视图,则该几何体外接球的表面积为( )| A. | 24π | B. | 29π | C. | 48π | D. | 58π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com