
分析 (1)利用等差数列的性质求出数列的首项与公差,然后求解通项公式.
(2)求出数列的前n项和,利用函数的单调性求解和的最小值即可.
解答 解 (1)由a2+a6=6,得a4=3,又由S5=$\frac{5({a}_{1}+{a}_{5})}{2}$=5a3=$\frac{35}{3}$,得a3=$\frac{7}{3}$,
设等差数列{an}的公差为d,则$\left\{\begin{array}{l}{{a}_{1}+2d=\frac{7}{3}}\\{{a}_{1}+3d=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=\frac{2}{3}}\end{array}\right.$,
∴an=$\frac{2}{3}$n+$\frac{1}{3}$.--------(7分)
(2)${S_n}=n{a_1}+\frac{n(n-1)}{2}d=n+\frac{n(n-1)}{3}=\frac{1}{3}({n^2}+2n)$----------(10分)
因为,${S_n}=\frac{1}{3}{(n+1)^2}-\frac{1}{3}$,当n≥1时,是单调递增的,
所以,当n=1时,Sn有最小值是S1=1.---------(14分)
点评 本题考查等差数列求和,通项公式的求法,数列的函数特征,考查计算能力.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
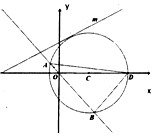 在平面直角坐标系中,已知圆C:x2+y2-4x-1=0与x轴正半轴的交点为D.
在平面直角坐标系中,已知圆C:x2+y2-4x-1=0与x轴正半轴的交点为D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1或2 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com