
���� ��1�����������ļ�������ɵ�$\overrightarrow{OP}$��$\overrightarrow{OQ}$���ٸ��������ε������ʽ�ͻ�������ʽ���������ֵ��
��2�����������ļ�������ɵ�|$\overrightarrow{OM}$|=$\frac{1}{4}$|$\overrightarrow{OP}$-$\overrightarrow{OQ}$|=$\frac{1}{4}$��4=1����ֵΪ������
��� �⣺��1��|$\overrightarrow{OP}$+$\overrightarrow{OQ}$|=|$\overrightarrow{OP}$-$\overrightarrow{OQ}$|=4
��$\overrightarrow{OP}$��$\overrightarrow{OQ}$��
��S��OPQ=$\frac{1}{2}$OP•OQ��$\frac{1}{2}$•��$\frac{OP+OQ}{2}$��2=$\frac{1}{2}$��$\frac{��OP+OQ��^{2}}{4}$=$\frac{1}{2}$��$\frac{16}{4}$=2��
��2����$\overrightarrow{QP}$=4$\overrightarrow{QM}$��
��$\overrightarrow{OM}$=$\frac{1}{4}$$\overrightarrow{QP}$=$\frac{1}{4}$��$\overrightarrow{OP}$-$\overrightarrow{OQ}$����
��|$\overrightarrow{OM}$|=$\frac{1}{4}$|$\overrightarrow{OP}$-$\overrightarrow{OQ}$|=$\frac{1}{4}$��4=1��
��|$\overrightarrow{OM}$|��ֵ�dz����������ֵ��
���� ���⿼���������ļ�������������ε������ʽ�ͻ�������ʽ�������е��⣮


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������$C��\frac{x^2}{m}+\frac{y^2}{n}=1��m��0��n��0��$��������L��|x|+|y|=4�ı߽����У�
��ͼ������$C��\frac{x^2}{m}+\frac{y^2}{n}=1��m��0��n��0��$��������L��|x|+|y|=4�ı߽����У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{1}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�Φ���m��n����n�ͦ� | B�� | ��m�ͦ���m��n����n�Φ� | ||
| C�� | ��m��n��m?����n?�£�����Φ� | D�� | ��m��n��m�ͦ���n�ͦ£�����Φ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
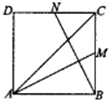
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����x��Ԫ�� | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| ����y������ | 90 | 84 | 83 | 80 | 75 | 68 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com