
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为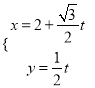 ,(
,( ![]() 为参数)
为参数)
(1)求曲线![]() 的参数方程和曲线
的参数方程和曲线![]() 的普通方程;
的普通方程;
(2)求曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的取值范围.
的距离的取值范围.
科目:高中数学 来源: 题型:
【题目】如图, ![]() 面
面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,它的制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立。某陶瓷厂准备仿制甲、乙、丙三件不同的唐三彩工艺品,根据该厂全面治污后的技术水平,经过第一次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() ,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() .
.
(1)求第一次烧制后甲、乙、丙三件中恰有一件工艺品合格的概率;
(2)经过前后两次烧制后,甲、乙、丙三件工艺品成为合格工艺品的件数为![]() ,求随机变量
,求随机变量![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数是定义在![]() ,
, ![]() ,
, ![]() 上的奇函数,当
上的奇函数,当![]() ,
, ![]() 时,
时, ![]() (
(![]() ).
).
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,
, ![]() ,
, ![]() ,求证:当
,求证:当![]() 时,
时, ![]() 恒成立;
恒成立;
(Ⅲ)是否存在实数![]() ,使得当
,使得当![]() ,
, ![]() 时,
时, ![]() 的最小值是
的最小值是![]() ?如果存在,
?如果存在,
求出实数![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)如图,已知椭圆![]() :
:![]() ,其左右焦点为
,其左右焦点为![]() 及
及![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 的中垂线与
的中垂线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.

(1)求椭圆![]() 的方程;
的方程;
(2)记△![]() 的面积为
的面积为![]() ,△
,△![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() .试问:是否存在直线
.试问:是否存在直线![]() ,使得
,使得![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂从今年一月起,若不改善生产环境,按生产现状,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月增加2万元.如果从今年一月起投资500万元添加回收净化设备(改造设备时间不计),一方面可以改善环境,另一方面也可以大大降低原料成本.据测算,添加回收净化设备并投产后的前5个月中的累计生产净收入![]() 是生产时间
是生产时间![]() 个月的二次函数
个月的二次函数![]() (
(![]() 是常数),且前3个月的累计生产净收入可达309万,从第6个月开始,每个月的生产净收入都与第5个月相同.同时,该厂不但不受处罚,而且还将得到环保部门的一次性奖励100万元.
是常数),且前3个月的累计生产净收入可达309万,从第6个月开始,每个月的生产净收入都与第5个月相同.同时,该厂不但不受处罚,而且还将得到环保部门的一次性奖励100万元.
(1)求前8个月的累计生产净收入![]() 的值;
的值;
(2)问经过多少个月,投资开始见效,即投资改造后的纯收入多于不改造时的纯收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
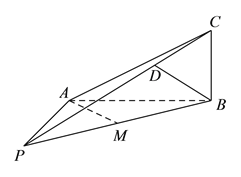
【题目】己知四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,且
是菱形,且![]() .
. ![]() ,
, ![]() 、
、![]() 的中点分别为
的中点分别为![]() ,
, ![]() .
.
(Ⅰ)求证![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平行于平面
平行于平面![]() ?若存在,指出
?若存在,指出![]() 在
在![]() 上的位置并给予证明,若不存在,请说明理由.
上的位置并给予证明,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com