
 ��������Ⱦָ������λ����g/m3��Ϊ0��50ʱ��������������Ϊһ������������״�������ţ���������Ⱦָ��Ϊ50��100ʱ��������������Ϊ��������������״������������������Ⱦָ��Ϊ100��150ʱ��������������Ϊ��������������״�����������Ⱦ����������Ⱦָ��Ϊ150��200ʱ��������������Ϊ�ļ�����������״�������ж���Ⱦ����������Ⱦָ��Ϊ200��300ʱ��������������Ϊ�弶����������״�������ض���Ⱦ����������Ⱦָ��Ϊ300����ʱ��������������Ϊ��������������״������������Ⱦ��ij��ijʡx����������ͳ�����£�
��������Ⱦָ������λ����g/m3��Ϊ0��50ʱ��������������Ϊһ������������״�������ţ���������Ⱦָ��Ϊ50��100ʱ��������������Ϊ��������������״������������������Ⱦָ��Ϊ100��150ʱ��������������Ϊ��������������״�����������Ⱦ����������Ⱦָ��Ϊ150��200ʱ��������������Ϊ�ļ�����������״�������ж���Ⱦ����������Ⱦָ��Ϊ200��300ʱ��������������Ϊ�弶����������״�������ض���Ⱦ����������Ⱦָ��Ϊ300����ʱ��������������Ϊ��������������״������������Ⱦ��ij��ijʡx����������ͳ�����£�| ������Ⱦָ������λ����g/m3�� | [0��50] | ��50��100] | ��100��150] | ��150��200] |
| ������� | 15 | 40 | y | 10 |
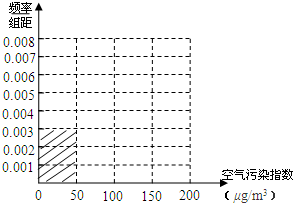
���� ��1����ֱ��ͼ���ص�ɵ�0.003��50=$\frac{15}{x}$���ɵ�xֵ�������ɵ�yֵ���ɵ������$\frac{Ƶ��}{���}$�������ֱ��ͼ��
��2����A�п�������״�����������Ⱦ3������Ϊ1��2��3����������״����������2������Ϊ4��5���оٿɵ��ܵĻ����¼���10�֣��¼�A����7�֣��ɸ��ʹ�ʽ�ɵ�
��� 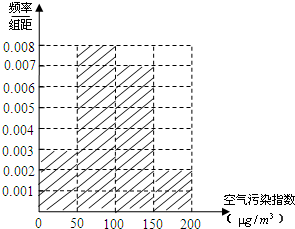 �⣺��1����$0.003��50=\frac{15}{x}��x=100$
�⣺��1����$0.003��50=\frac{15}{x}��x=100$
��15+40+y+10=100����y=35
$\frac{40}{100��50}=0.008$
$\frac{35}{100��50}=0.007$
$\frac{10}{100��50}=0.002$
��2����A�п�������״�����������Ⱦ3������Ϊ1��2��3����������״����������2������Ϊ4��5��
������ȡ2���Ļ����¼��ֱ�Ϊ
��1��2������1��3������1��4������1��5����
��2��3������2��4������2��5������3��4������3��5������4��5����10�֣�
�����¼�A������������һ��Ϊ���������� �����¼�Ϊ
��1��4������1��5������2��4������2��5������3��4������3��5������4��5����7�֣�
�����¼�A������������һ��Ϊ���������ĸ�����$P��A��=\frac{7}{10}$��
���� ���⿼���оٷ���������¼������¼������ĸ��ʣ��漰Ƶ�ʷֲ�ֱ��ͼ���������⣮


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��n=2k+1ʱ��ȷ������n=2k+3��ȷ | |
| B�� | ��n=2k-1ʱ��ȷ������n=2k+1ʱ��ȷ | |
| C�� | ��n=kʱ��ȷ������n=k+2ʱ��ȷ | |
| D�� | ��n��k��k��1����ȷ������n=k+2ʱ��ȷ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ִ����ͼ��ʾ�ij����ͼ����������t=0.01���������n=��������
ִ����ͼ��ʾ�ij����ͼ����������t=0.01���������n=��������| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 010 | C�� | 4 018 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com