
【题目】如图所示,四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
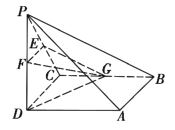
(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明略;
(2)![]()
【解析】(1)证法1:∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() 为正方形,∴
为正方形,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .……………………………………………3分
.……………………………………………3分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .…………………………………………………………6分
.…………………………………………………………6分
证法2:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,则
,则![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .………4分
.………4分
∵![]() ,∴
,∴![]() .………6分
.………6分
(2)解法1:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,……………8分
,……………8分
设平面DFG的法向量为![]() ,
,
∵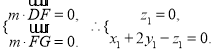
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.…………………………10分
的一个法向量.…………………………10分
设平面EFG的法向量为![]() ,
,
∵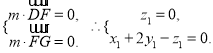
令![]() ,得
,得![]() 是平面
是平面![]() 的一个法向量.……………………………12分
的一个法向量.……………………………12分
∵ .
.
设二面角![]() 的平面角为θ,则
的平面角为θ,则![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .………………………………………14分
.………………………………………14分
解法2:以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,W
,W
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() .………………………………8分
.………………………………8分
过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() 三点共线,∴
三点共线,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
即![]() ,解得
,解得![]() .
.
∴![]() .………………………………………………10分
.………………………………………………10分
再过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
∵![]() 三点共线,∴
三点共线,∴![]() ,
,
∵![]() ,∴
,∴![]()
![]() ,
,
即![]() ,解得
,解得![]() .
.
∴![]() .……………………………………………12分
.……………………………………………12分
∴ .
.
∵![]() 与
与![]() 所成的角就是二面角
所成的角就是二面角![]() 的平面角,
的平面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .………………………………………14分
.………………………………………14分



 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度,研究人员在![]() 地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中
地各个国企中随机抽取了1000名员工进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.
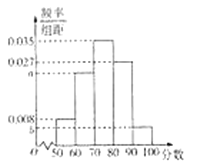
(Ⅰ)估计被调查的员工的满意程度的中位数;(计算结果保留两位小数)
(Ⅱ)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取4人,记分数在
中随机抽取8人,再从这8人中随机抽取4人,记分数在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
(Ⅲ)以频率估计概率,若该研究人员从全国国企员工中随机抽取![]() 人作调查,记成绩在
人作调查,记成绩在![]() ,
,![]() 的人数为
的人数为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半圆![]() :
:![]() ,
,![]() 、
、![]() 分别为半圆
分别为半圆![]() 与
与![]() 轴的左、右交点,直线
轴的左、右交点,直线![]() 过点
过点![]() 且与
且与![]() 轴垂直,点
轴垂直,点![]() 在直线
在直线![]() 上,纵坐标为
上,纵坐标为![]() ,若在半圆
,若在半圆![]() 上存在点
上存在点![]() 使
使![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)袋中装有黑色球和白色球共7个,从中任取2个球都是白色球的概率为![]() .现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
.现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
(1)求随机变量X的分布列和均值E(X);
(2)求甲摸到白色球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() .
.
(1)若![]() ,写出
,写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)设![]() ,若
,若![]() ,求
,求![]() 的值及
的值及![]() 时数列
时数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)求证:“数列![]() 是等差数列”的充要条件是“数列
是等差数列”的充要条件是“数列![]() 是等差数列”.
是等差数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知U=R且A={x|a2x2-5ax-6<0},B{x||x-2|≥1}.
(1)若a=1,求(UA)![]() B;
B;
(2)求不等式a2x2-5ax-6<0(a∈R)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
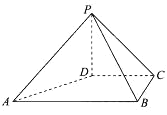
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:只要
满足:只要![]() ,必有
,必有![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)若![]() 具有性质
具有性质![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列, ![]() ,
, ![]() ,
, ![]() 判断
判断![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(3)设![]() 是无穷数列,已知
是无穷数列,已知![]() .求证:“对任意
.求证:“对任意![]() 都具有性质
都具有性质![]() ”的充要条件为“
”的充要条件为“![]() 是常数列”.
是常数列”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com