
分析 (1)由题意知e=$\frac{c}{a}$=$\frac{1}{2}$,$\frac{{\sqrt{3}}^{2}}{{a}^{2}}$+$\frac{(\frac{\sqrt{3}}{2})^{2}}{{b}^{2}}$=1,从而解得椭圆方程;结合图象求面积;
(2)由题意设直线AC的方程为x=$\frac{y}{{k}_{1}}$+t,从而与椭圆方程联立化简可得(4+$\frac{3}{{{k}^{2}}_{1}}$)y2+6t$\frac{1}{{k}_{1}}$x+3t2-12=0,从而可得|AT|•|TC|=(1+$\frac{1}{{{k}^{2}}_{1}}$)•|y1y2|=(1+$\frac{1}{{{k}^{2}}_{1}}$)•|$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{1}}}$|,|BT|•|TD|=(1+$\frac{1}{{{k}^{2}}_{2}}$)•|$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{2}}}$|,从而证明.
解答 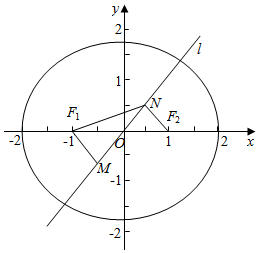 解:(1)∵e=$\frac{c}{a}$=$\frac{1}{2}$,$\frac{{\sqrt{3}}^{2}}{{a}^{2}}$+$\frac{(\frac{\sqrt{3}}{2})^{2}}{{b}^{2}}$=1,
解:(1)∵e=$\frac{c}{a}$=$\frac{1}{2}$,$\frac{{\sqrt{3}}^{2}}{{a}^{2}}$+$\frac{(\frac{\sqrt{3}}{2})^{2}}{{b}^{2}}$=1,
∴a2=4,c2=1,b2=3;
∴椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
结合图象可知,
|OF1|=1,∠F1OM=$\frac{π}{4}$;
|MF1|=|OM|=$\frac{\sqrt{2}}{2}$,
故S${\;}_{△{F}_{1}MN}$=$\frac{1}{2}$•|MN|•|MF1|
=$\frac{1}{2}$•$\sqrt{2}$•$\frac{\sqrt{2}}{2}$=$\frac{1}{2}$;
证明:(2)由题意,设直线AC的方程为x=$\frac{y}{{k}_{1}}$+t,
与$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1联立消元可得,
(4+$\frac{3}{{{k}^{2}}_{1}}$)y2+6t$\frac{1}{{k}_{1}}$x+3t2-12=0,
设A(x1,y1),C(x2,y2)
∴y1y2=$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{1}}}$,
∴|AT|•|TC|=(1+$\frac{1}{{{k}^{2}}_{1}}$)•|y1y2|=(1+$\frac{1}{{{k}^{2}}_{1}}$)•|$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{1}}}$|,
同理可得,
|BT|•|TD|=(1+$\frac{1}{{{k}^{2}}_{2}}$)•|$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{2}}}$|,
故(1+$\frac{1}{{{k}^{2}}_{1}}$)•|$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{1}}}$|=(1+$\frac{1}{{{k}^{2}}_{2}}$)•|$\frac{3{t}^{2}-12}{4+\frac{3}{{{k}^{2}}_{2}}}$|;
故(1+$\frac{1}{{{k}^{2}}_{1}}$)(4+$\frac{3}{{{k}^{2}}_{2}}$)=(1+$\frac{1}{{{k}^{2}}_{2}}$)(4+$\frac{3}{{{k}^{2}}_{1}}$),
故$\frac{1}{{{k}^{2}}_{1}}$=$\frac{1}{{{k}^{2}}_{2}}$;
故k1=k2(舍去)或k1=-k2;
故k1+k2=0,为定值.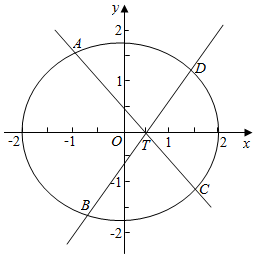
点评 本题考查了圆锥曲线与直线的位置关系的应用及判断,同时考查了数形结合的思想方法应用,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x>0) | B. | $\frac{x^2}{16}-\frac{y^2}{9}$=1 | C. | $\frac{x^2}{16}-\frac{y^2}{9}$=1(x<0) | D. | $\frac{x^2}{25}+\frac{y^2}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{21}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
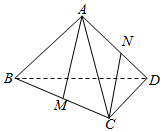 空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )
空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0} | B. | {x|x≥2} | C. | {x|x<0或x>2} | D. | {x|x≤0或x≥2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com