
| A. | $\sqrt{2}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
分析 利用双曲线的对称性及直角三角形,可得∠MF2F1=45°,从而|MF1|=|F1F2|,求出关于a,b,c的等式,即可求出离心率的值.
解答 解:∵△MF2N是等腰直角三角形,∴∠MF2N为直角,
∵双曲线关于x轴对称,且直线MN垂直x轴,
∴∠MF2F1=45°,
∴|MF1|=|F1F2|,∵F为左焦点,设其坐标为(-c,0),
令x=-c,则有y=±$\frac{{b}^{2}}{a}$,
∴|MF1|=$\frac{{b}^{2}}{a}$=2c,∴c2-2ac-a2=0
∴e2-2e-1=0
∵e>1,∴e=1+$\sqrt{2}$.
故选:C.
点评 本题考查双曲线的对称性、考查双曲线的三参数关系:c2=a2+b2、考查双曲线的离心率,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=1-x | B. | y=-|x| | C. | $y=\frac{1}{x-1}$ | D. | $y={x^{\frac{1}{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | sinα | C. | -tanα | D. | tanα |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
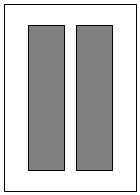 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com