
分析 利用列举法得到同时向上掷两枚骰子,向上的点数之和共有36种结果,而向上的点数之和为5的结果有4种情况,由此能求出向上的点数之和等于5的概率.
解答 解:记“同时向上掷两枚骰子,向上的点数之和等于5”为事件A,
∵同时向上掷两枚骰子,向上的点数之和共有以下36种结果:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
而向上的点数之和为5的结果有(4,1),(3,2),(2,3),(1,4)等4种情况
∴P(A)=$\frac{4}{36}$=$\frac{1}{9}$,
故一颗骰子连续抛掷2次,向上的点数之和等于5的概率为$\frac{1}{9}$,
故答案为:$\frac{1}{9}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
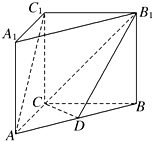 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 将边长分别为1、2、3、4、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,an+1=$\left\{\begin{array}{l}f(n)\;\;当n为奇数\\ f({a_n})当n为偶数\end{array}$.
将边长分别为1、2、3、4、…、n、n+1、…(n∈N*)的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为f(n).记数列{an}满足a1=1,an+1=$\left\{\begin{array}{l}f(n)\;\;当n为奇数\\ f({a_n})当n为偶数\end{array}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}{,^{\;}}\frac{1}{2}$ | B. | $\frac{3}{5}{,^{\;}}\frac{3}{5}$ | C. | $\frac{1}{2}{,^{\;}}\frac{1}{2}$ | D. | $\frac{3}{5}{,^{\;}}\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com