
分析 (1)ξ的不同取值为0,1,2,3,4.P(ξ=k)=$\frac{{∁}_{6}^{5-k}{∁}_{4}^{k}}{{∁}_{10}^{5}}$(k=0,1,2,3,4),进而得出E(ξ).
(2)因为每道题答对与否相互没有影响,所以甲选定的5道题之间是独立的.设甲取得良好成绩的事件为A,P(A)=${C_5}^4×{0.6^4}×0.4+{C_5}^5×{0.6^5}$,则甲没有得到良好成绩的概率为:1-P(A).
解答 解:(1)ξ的不同取值为0,1,2,3,4.P(ξ=k)=$\frac{{∁}_{6}^{5-k}{∁}_{4}^{k}}{{∁}_{10}^{5}}$(k=0,1,2,3,4),
P(ξ=0)=$\frac{1}{42}$,P(ξ=1)=$\frac{5}{21}$,P(ξ=2)
=$\frac{10}{21}$,P(ξ=3)=$\frac{5}{21}$,P(ξ=4)=$\frac{1}{42}$.
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{42}$ | $\frac{5}{21}$ | $\frac{10}{21}$ | $\frac{5}{21}$ | $\frac{1}{42}$ |
点评 本题考查了相互独立、超几何分布列及其概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 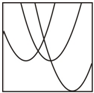 | B. | 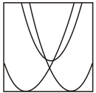 | C. | 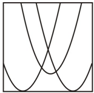 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 3f(4)<4f(3) | C. | $\frac{f(3)}{4}>\frac{f(4)}{3}$ | D. | f(2)<2f(1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com