
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
分析 设球心为O,作AB中点D,连结OD、CD,由棱锥S-ABC的体积V=$\frac{1}{3}×AB×{S}_{△SCD}$,利用余弦定理、三角形面积公式,能求出三棱锥S-ABC的体积.
解答 解:设球心为O,作AB中点D,连结OD、CD,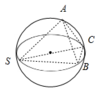
∵线段SC是球的直径,∴SC是大圆的直径,
∴∠SAC=∠SBC=90°,
∴在Rt△SAC中,SC=4,∠ASC=30°,∴AC=2,SA=2$\sqrt{3}$,
又在Rt△SBC中,SC=4,∠ASC=30°,∴BC=2,SB=2$\sqrt{3}$,
∴SA=SB,AC=BC,
∵点D是AB的中点,∴在等腰△ASB中,SD⊥AB,且SD=$\sqrt{S{A}^{2}-A{D}^{2}}$=$\sqrt{12-\frac{3}{4}}$=$\frac{3\sqrt{5}}{2}$,
在等腰△CAB中,CD⊥AB,且CD=$\sqrt{A{C}^{2}-A{D}^{2}}=\sqrt{4-\frac{3}{4}}=\frac{\sqrt{13}}{2}$,
又SD∩CD=D,∴AB⊥平面SCD,即棱锥S-ABC的体积V=$\frac{1}{3}×AB×{S}_{△SCD}$,
∵SD=$\frac{3\sqrt{5}}{2}$,CD=$\frac{\sqrt{13}}{2}$,
∴由余弦定理得cos∠SDC=$\frac{S{D}^{2}+C{D}^{2}-S{C}^{2}}{2×SD×CD}$=$\frac{\frac{45}{4}+\frac{13}{4}-16}{2×\frac{3\sqrt{5}}{2}×\frac{\sqrt{13}}{2}}$=-$\frac{1}{\sqrt{65}}$,
∴sin$∠SDC=\sqrt{1-(-\frac{1}{65}})^{2}$=$\frac{8}{\sqrt{65}}$,
∴由三角形面积公式得△SCD的面积:
S=$\frac{1}{2}×SD×CD×sin∠SDC$=$\frac{1}{2}×\frac{3\sqrt{5}}{2}×\frac{\sqrt{13}}{2}×\frac{8}{\sqrt{65}}$=3,
∴三棱锥S-ABC的体积为:
V=$\frac{1}{3}×AB×{S}_{△SCD}$=$\frac{1}{3}×AB×{S}_{△SCD}$=$\frac{1}{3}×\sqrt{3}×3$=$\sqrt{3}$.
点评 本题考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意余弦定理、三角形面积公式、球的性质的合理运用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:解答题
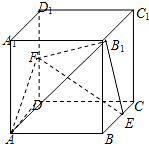 棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.
棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
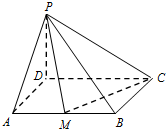 如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.
如图,在四棱锥P-ABCD中,已知底面ABCD是矩形,AB=2,AD=a,PD⊥平面ABCD,若边AB上有且只有一点M,使得PM⊥CM,则实数a=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.
已知线段AB上有9个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),…,这样一直继续下去,直到1,2,3,…,2013都被标记到点上.则点2013上的所有标记的数中,最小的是2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某工厂生产A,B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品,为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示:
某工厂生产A,B两种型号的产品,每种型号的产品在出厂时按质量分为一等品和二等品,为便于掌握生产状况,质检时将产品分为每20件一组,分别记录每组一等品的件数.现随机抽取了5组的质检记录,其一等品数茎叶图如图所示: | 一等品 | 二等品 |
| A型 | 4(万元) | 3(万元) |
| B型 | 3(万元) | 2(万元) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
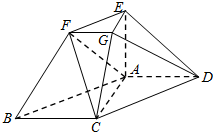 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com