Question

11．已知函数y=sin（2x-$\frac{π}{6}$）-m在[$\frac{π}{2}$，π]上有两个零点，则m的取值范围为（　　）

• A． [$\frac{1}{2}，1$]
• B． [-1，-$\frac{1}{2}$]
• C． [$\frac{1}{2}，1$）
• D． （-1，-$\frac{1}{2}$]

Answer 1

分析 根据正弦函数的性质，求出y=sin（2x-$\frac{π}{6}$）在[$\frac{π}{2}$，π]上图象，由题意，函数y=sin（2x-$\frac{π}{6}$）-m在[$\frac{π}{2}$，π]上有两个零点，即它们图象有两个交点．利用数形结合法求解即可．

解答 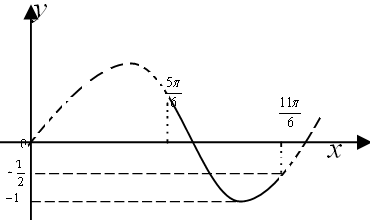解：∵x在[$\frac{π}{2}$，π]上，
∴（2x-$\frac{π}{6}$）∈[$\frac{5π}{6}$，$\frac{11π}{6}$]，
令2x-$\frac{π}{6}$=t，
则t∈[$\frac{5π}{6}$，$\frac{11π}{6}$]，
那么y=sint的图象与y=m两个交点，
当t=$\frac{7π}{6}$或$\frac{11π}{6}$时，y=$-\frac{1}{2}$，
由图象可知：
m在（-1，-$\frac{1}{2}$]时，函数y=m与函数y=sint即y=sin（2x-$\frac{π}{6}$）两个交点，即有两个零点．
故选D．

点评 本题主要考察了三角函数的图象及性质的运用和与函数y=m的零点即交点问题．属于基础题．