
分析 可以用来衡量模拟效果好坏的几个量分别是相关指数,残差平方和和相关系数,只有残差平方和越小越好,其他的都是越大越好.
解答 解:①相关系数r的绝对值越趋近于1,相关性越强;越趋近于0,相关性越弱,故错误;
②残差平方和越小,模型拟合的效果越好,故错误;
③用相关指数R2来刻画回归效果时,R2越大,说明模型的拟合效果越好;
④用最小二乘法求回归直线方程,是寻求使$\sum_{i=1}^n{{{({y_i}-b{x_i}-a)}^2}}$取最小值时的a,b的值,根据用最小二乘法求回归直线方程的方法,可知正确;
⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
故答案为④⑤.
点评 本题主要考查线性相关指数的理解,解题的关键是理解对于拟合效果好坏的几个量的大小反映的拟合效果的好坏,比较基础.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
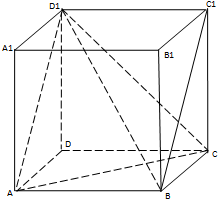 如图在正方体中
如图在正方体中查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com