
分析 由题意知奖金X的所有可能取值为0,300,600,2400,顾客抽奖一次,基本事件总数为${∁}_{10}^{3}$=120,三球号码有且仅有两个连号的情况中,对应1,2与9,10的各有7种;对应2,3;…;8,9各有6种.可得P(X=300),三球号码都连号为二等奖,只有1,2,3;2,3,4;…;8,9,10,共有8种情况,可得P(X=600);一等奖只有一种情况,可得P(X=2400),利用对立事件的概率计算公式可得P(X=0)=1-P(X=300)-P(X=600)-P(X=2400),进而得出数学期望.
解答 解:由题意知奖金X的所有可能取值为0,300,600,2400,
顾客抽奖一次,基本事件总数为${∁}_{10}^{3}$=120,
三球号码有且仅有两个连号的情况中,对应1,2与9,10的各有7种;对应2,3;…;8,9各有6种.
∴P(X=300)=$\frac{7×2+6×7}{120}$=$\frac{7}{15}$,
三球号码都连号为二等奖,只有1,2,3;2,3,4;…;8,9,10,共有8种情况,∴P(X=600)=$\frac{8}{120}$=$\frac{1}{15}$,
一等奖只有一种情况,∴P(X=2400)=$\frac{1}{120}$,
P(X=0)=1-$\frac{7}{15}$-$\frac{1}{15}$-$\frac{1}{120}$=$\frac{11}{24}$.
∴X的分布列为:
| X | 0 | 300 | 600 | 2400 |
| P | $\frac{11}{24}$ | $\frac{7}{15}$ | $\frac{1}{15}$ | $\frac{1}{120}$ |
点评 本题考查了古典概率计算公式及其随机变量的数学期望,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
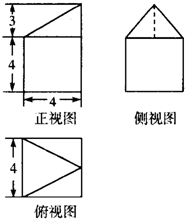
| A. | 98+6$\sqrt{5}$ | B. | 106+6$\sqrt{5}$ | C. | 114+6$\sqrt{5}$ | D. | 106+12$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
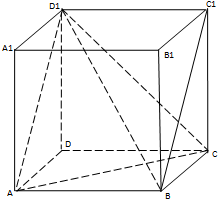 如图在正方体中
如图在正方体中查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com