
| A. | $\frac{3}{5}{,^{\;}}\frac{1}{2}$ | B. | $\frac{3}{5}{,^{\;}}\frac{3}{5}$ | C. | $\frac{1}{2}{,^{\;}}\frac{1}{2}$ | D. | $\frac{3}{5}{,^{\;}}\frac{2}{5}$ |
分析 利用互斥事件概率加法公式和相互独立事件概率乘法公式能求出x;利用条件概率计算公式能求出y.
解答 解:∵在五张牌中有三张K和两张A,如果不放回地一次抽取两张牌.
记“第2次抽到扑克牌K的概率为x”,
“在第一次抽到扑克牌K的条件下,第二次抽到扑克牌K的概率为y”,
∴x=$\frac{3}{5}×\frac{2}{4}+\frac{2}{5}×\frac{3}{4}$=$\frac{3}{5}$,
y=$\frac{\frac{3}{5}×\frac{2}{4}}{\frac{3}{5}}$=$\frac{1}{2}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式、相互独立事件概率乘法公式、条件概率计算公式的合理运用.


科目:高中数学 来源: 题型:填空题
| Z | 1 | 2 | 3 |
| P | 0.5 | x | y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 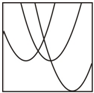 | B. | 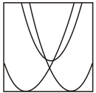 | C. | 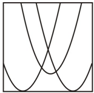 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com