
分析 (1)已知第一个等式利用两角和与差的正切函数公式化简求出tanα的值,原式利用二倍角的正切函数公式化简后,代入计算即可求出值;
(2)原式利用两角和与差的正弦、余弦函数公式化简,再利用同角三角函数间基本关系变形,将已知等式代入计算即可求出值.
解答 解:(1)∵tan($\frac{π}{4}$+α)=$\frac{1+tanα}{1-tanα}$=2,
∴tanα=$\frac{1}{3}$,
则tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{\frac{2}{3}}{1-\frac{1}{9}}$=$\frac{3}{4}$;
(2)∵tanα=$\frac{1}{3}$,tanβ=$\frac{1}{2}$,
∴原式=$\frac{sinαcosβ+cosαsinβ-2sinαcosβ}{2sinαsinβ+cosαcosβ-sinαsinβ}$=$\frac{cosαsinβ-sinαcosβ}{sinαsinβ+cosαcosβ}$=$\frac{tanβ-tanα}{tanαtanβ+1}$=$\frac{\frac{1}{2}-\frac{1}{3}}{\frac{1}{2}×\frac{1}{3}+1}$=$\frac{1}{7}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.


科目:高中数学 来源: 题型:解答题
 如图所示,AB是圆O的直径,BC与圆O相切于B,D为圆O上一点,∠ADC+∠DCO=180°.
如图所示,AB是圆O的直径,BC与圆O相切于B,D为圆O上一点,∠ADC+∠DCO=180°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组号 | 分组 | 回答 正确 的人数 | 回答正确 的人数占本 组的频率 | 频率正确直方图 |
| 第1组 | [15,25) | 5 | 0.5 | 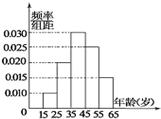 |
| 第2组 | [25,35) | a | 0.9 | |
| 第3组 | [35,45) | 27 | x | |
| 第4组 | [45,55) | 9 | 0.36 | |
| 第5组 | [55,65) | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
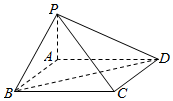 如图,在四棱锥P-ABCD中,ABCD是菱形,PA⊥平面ABCD
如图,在四棱锥P-ABCD中,ABCD是菱形,PA⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
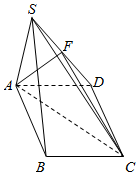 已知在四棱锥S-ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点.
已知在四棱锥S-ABCD中,底面ABCD是菱形,且∠BCD=60°,侧面SAB是正三角形,且面SAB⊥面ABCD,F为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
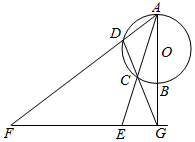 如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F.求证:
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com