
分析 构造将二次函数f(x)=x2+ax+4,利用二次函数的图象和性质求解,要使不等式f(x)<0恒成立,则只需求出函数在x∈[1,2)时的最大值即可.
解答 解:令f(x)=x2+ax+4,
则由二次函数的图象和性质可知,
当1≤x<2时,
不等式x2+ax+4<0恒成立等价于,$\left\{\begin{array}{l}{f(1)<0}\\{f(2)≤0}\end{array}\right.$,
即 $\left\{\begin{array}{l}{1+a+4<0}\\{4+2a+4≤0}\end{array}\right.$,
解得,a<-5,
∴实数a的取值范围(-∞,-5)
点评 本题主要考查二次函数的图象和性质在研究一元二次不等式中的应用,属于中档题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x<-$\frac{1}{3}$或x>$\frac{1}{2}$} | C. | {x|-$\frac{1}{2}$<x<$\frac{1}{3}$} | D. | {x|x<-$\frac{1}{2}$或x>$\frac{1}{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
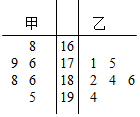 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com