
| A. | (-∞,2)和(3,+∞) | B. | (2,3) | C. | (-1,6) | D. | (-3,-2) |
分析 对函数f(x)=-$\frac{1}{3}}$x3+$\frac{5}{2}}$x2-6x+5进行求导,然后令导函数小于0求出x的范围,即可得到答案.
解答 解:对函数f(x)=-$\frac{1}{3}}$x3+$\frac{5}{2}}$x2-6x+5求导,得f′(x)=-x2+5x-6,
令f′(x)>0,即-x2+5x-6>0,可得x2-5x+6<0,解得,2<x<3,
∴函数f(x)=-$\frac{1}{3}}$x3+$\frac{5}{2}}$x2-6x+5的单调增区间为:(2,3).
故选:B.
点评 本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
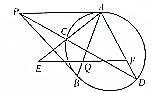 如图,过圆外一点P作圆的两条切线PA、PB,A,B为切点,再过P点作圆的一条割线分别与圆交于点C、D,过AB上任一点Q作PA的平行线分别与直线AC、AD交于点E,F,证明:QE=QF.
如图,过圆外一点P作圆的两条切线PA、PB,A,B为切点,再过P点作圆的一条割线分别与圆交于点C、D,过AB上任一点Q作PA的平行线分别与直线AC、AD交于点E,F,证明:QE=QF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com