
分析 讨论a的取值:a<2,2≤a≤3,a>3,三种情况,求出每种情况下的f(x)的最小值,让最小值大于等于0从而求出a的取值范围.
解答 解:f(x)=x|x-a|-a;
∴①若a<2,则x=2时,f(x)在[2,3]上取得最小值f(2)=2(2-a)-a=4-3a;
∴4-3a≥0,a≤$\frac{4}{3}$;
∴a≤$\frac{4}{3}$;
②若2≤a≤3,则x=a时,f(x)取得最小值f(a)=-a;
-a<0,不满足f(x)≥0;
即这种情况不存在;
③若a>3,则x=3时,f(x)取得最小值f(3)=3(a-3)-a=2a-9;
∴2a-9≥0,a≥$\frac{9}{2}$;
∴a≥$\frac{9}{2}$;
综上得a的取值范围为:(-∞,$\frac{4}{3}$]∪[$\frac{9}{2}$,+∞).
点评 考查奇函数的定义,奇函数在原点有定义时f(0)=0,函数零点的定义,含绝对值函数求最值的方法:观察解析式的方法,以及画出分段函数的图象,以及根据图象求函数零点个数的方法.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充分必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
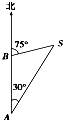 (文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.
(文)如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8$\sqrt{2}$ n mile.求此船的航速.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 真,假,真 | B. | 假,假,真 | C. | 真,真,假 | D. | 假,假,假 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com