
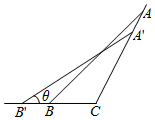
 在△ABC中,角A、B、C所对的边分别是a、b、c.若∠C=$\frac{2}{3}$π,a、b、c依次成等差数列,且公差为2,如图.A′B′分别在射线CA,CB上运动,且满足A′B′=AB,设∠A′B′C′=θ,则△A′CB′周长最大值为7+$\frac{14\sqrt{3}}{3}$.
在△ABC中,角A、B、C所对的边分别是a、b、c.若∠C=$\frac{2}{3}$π,a、b、c依次成等差数列,且公差为2,如图.A′B′分别在射线CA,CB上运动,且满足A′B′=AB,设∠A′B′C′=θ,则△A′CB′周长最大值为7+$\frac{14\sqrt{3}}{3}$. 分析 由题意得知b=a+2,c=a+4,∠C=$\frac{2}{3}$π,从而利用余弦定理求得边长,再由正弦定理求得各边长,从而求周长即可.
解答 解:由题意得,
b=a+2,c=a+4,∠C=$\frac{2}{3}$π,
∴(a+4)2=a2+(a+2)2-2a(a+2)cos$\frac{2}{3}$π,
解得,a=3或a=-2(舍去),
故a=3,b=5,c=7,
∵$\frac{A′B′}{sin\frac{π}{3}}$=$\frac{A′C}{sinθ}$=$\frac{B′C}{sin(\frac{π}{3}-θ)}$,
∴A′C=$\frac{14\sqrt{3}}{3}$sinθ,B′C=$\frac{14\sqrt{3}}{3}$sin($\frac{π}{3}$-θ),
∴△A′CB′周长l=7+$\frac{14\sqrt{3}}{3}$sinθ+$\frac{14\sqrt{3}}{3}$sin($\frac{π}{3}$-θ)
=7+$\frac{14\sqrt{3}}{3}$•2•sin$\frac{π}{6}$cos(θ-$\frac{π}{6}$),
故当θ=$\frac{π}{6}$时有最大值为
7+$\frac{14\sqrt{3}}{3}$•2•$\frac{1}{2}$=7+$\frac{14\sqrt{3}}{3}$;
故答案为:7+$\frac{14\sqrt{3}}{3}$.
点评 本题考查了解三角形的应用及三角函数的化简运算,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤3} | B. | {1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
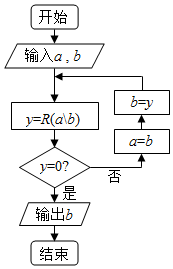 “辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )
“辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com