练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．求方程4sin2x-2sinxcosx-1=0的解集．

    分析 原方程可化为（sinx-cosx）（3sinx+cosx）=0，可得tanx，由反三角函数可得．

    解答 解：原方程4sin2x-2sinxcosx-1=0可化为3sin2x-2sinxcosx+sin2x-1=0，
    即3sin2x-2sinxcosx-cos2x=0，分解因式可得（sinx-cosx）（3sinx+cosx）=0，
    ∴sinx-cosx=0或3sinx+cosx=0，∴tanx=1或tanx=-$\frac{1}{3}$，
    ∴方程4sin2x-2sinxcosx-1=0的解集为{x|x=kπ+$\frac{π}{4}$或x=kπ-arctan$\frac{1}{3}$，k∈Z}．

    点评 本题考查三角函数恒等变换，变形并分解因式是解决问题的关键，属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知实数x，y满足$\left\{\begin{array}{l}x-y+1≥0\\ x-3y-1≤0\\ x≤1\end{array}\right.$，若z=kx-y的最小值为-5，则实数k的值为（　　）
    A．-3B．3或-5C．-3或-5D．±3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知等比数列{an}的第一项是$\frac{9}{8}$，最后一项是$\frac{1}{3}$．且各项的和是$\frac{65}{24}$．
    求：（1）这个等比数列的公比q；
    （2）这个等比数列的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若集合U={x∈N*|x≤6}，S={1，4，5}，T={2，3，4}，则S∩（∁UT）=（　　）
    A．{1，4，5，6}B．{1，5}C．{1，4}D．{1，2，3，4，5}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=2cos2x+sin（2x-$\frac{π}{6}$）-1．（x∈R）．
    （1）求函数f（x）的最小正周期及单调递增区间；
    （2）在△ABC中，三内角A，B，C的对边分别为a，b，c，已知函数f（x）的图象经过点（A，$\frac{1}{2}$），若b+c=2a，$\overrightarrow{AB}$•$\overrightarrow{AC}$=6，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

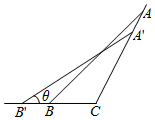    9．在△ABC中，角A、B、C所对的边分别是a、b、c．若∠C=$\frac{2}{3}$π，a、b、c依次成等差数列，且公差为2，如图．A′B′分别在射线CA，CB上运动，且满足A′B′=AB，设∠A′B′C′=θ，则△A′CB′周长最大值为7+$\frac{14\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设x＞0，y＞0，且（$\frac{x-y}{2}$）2=$\frac{4}{xy}$，则当x+y取最小值时，x2+y2=（　　）
    A．24B．22C．16D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．若a是从区间[0，3]上任取的一个数，b是从区间[0，2]上任取的一个数，求关于x的一元二次方程x2+2x+b=0有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在△ABC中，角A，B，C所对的边分别为a，b，c．若$bcosC+\frac{c}{{\sqrt{3}}}sinB=a$．
    （1）求角B的大小；
    （2）若△ABC的面积为$\sqrt{3}$，试求边b的最小值．

    查看答案和解析>>

    同步练习册答案