
分析 (1)根据条件建立方程关系即可求这个等比数列的公比q;
(2)根据等比数列的通项公式即可求这个等比数列的通项公式.
解答 解:∵等比数列{an}的第一项是$\frac{9}{8}$,最后一项是$\frac{1}{3}$.且各项的和是$\frac{65}{24}$.
∴$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{\frac{9}{8}(1-{q}^{n})}{1-q}$=$\frac{65}{24}$.
即65(1-q)=27(1-qn),①
∵an=a1qn-1,
∴$\frac{9}{8}$qn-1=$\frac{1}{3}$,即qn-1=$\frac{8}{27}$,
即qn=$\frac{8}{27}$q,代入①得65(1-q)=27(1-$\frac{8}{27}$q)=27-8q,
得57q=38,即q=$\frac{2}{3}$,则($\frac{2}{3}$)n-1=$\frac{8}{27}$=($\frac{2}{3}$)3,
即n-1=3,得n=4.
(2)∵q=$\frac{2}{3}$,a1=$\frac{9}{8}$,
∴an=($\frac{9}{8}$)•($\frac{2}{3}$)n-1=($\frac{3}{2}$)3•($\frac{2}{3}$)n-1=($\frac{2}{3}$)n-4.
点评 本题主要考查等比数列的通项公式以及等比数列的应用,根据条件建立方程关系是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
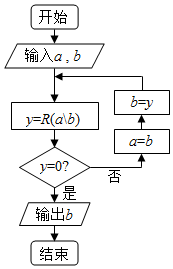 “辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )
“辗转相除法”的算法思路如图所示,记R(a\b)为a除以b所得的余数(a,b∈N*),执行如图的程序框图,若输入a,b分别为405,75,则输出b的值为( )| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com