【题目】设等差数列
的前
项和为
，数列
的前项和为
，下列说法错误的是（ ）
A. 若有最大值，则也有最大值
B. 若有最大值，则也有最大值
C. 若数列
不单调，则数列
也不单调
D. 若数列不单调，则数列也不单调
【答案】C
【解析】
根据等差数列的性质知数列{a2n﹣1}的首项是a1，公差为2d，结合等差数列的前n项和公式以及数列的单调性和最值性与首项公差的关系进行判断即可．
解：数列{a2n﹣1}的首项是a1，公差为2d，
A．若Sn有最大值，则满足a1＞0，d＜0，则2d＜0，即Tn也有最大值，故A正确，
B．若Tn有最大值，则满足a1＞0，2d＜0，则d＜0，即Sn也有最大值，故B正确，
C．Sn＝na1
d
n2+（a1
）n，对称轴为n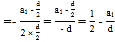
，
Tn＝na12d＝dn2+（a1﹣d）n，对称轴为n
，
不妨假设d＞0，
若数列{Sn}不单调，此时对称轴n
，即
1，
此时Tn的对称轴n
1，则对称轴
有可能成立，此时数列{Tn}有可能单调递增，
故C错误，
D．不妨假设d＞0，若数列{Tn}不单调，此时对称轴n
，即2，
此时{Sn}的对称轴n
2
，即此时{Sn}不单调，故D正确
则错误是C，
故选：C．
科目：高中数学 来源： 题型：
【题目】给出下列四个命题：
①命题“x∈R，cosx>0”的否定是“x0∈R，cosx0≤0”；
②若0<a<1，则函数f(x)＝x2＋ax－3只有一个零点；
③函数y＝2
sinxcosx在
上是单调递减函数；
④若lga＋lgb＝lg(a＋b)，则a＋b的最小值为4.
其中真命题的序号是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
过点
，且离心率为
.过抛物线
上一点
作
的切线
交椭圆
于
，
两点.
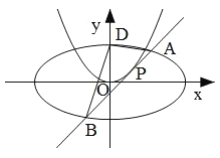
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在直线，使得
，若存在，求出的方程；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，下列四个结论不成立的是 ( )
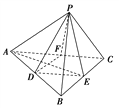
A. BC∥平面PDF B. DF⊥平面PAE
C. 平面PDF⊥平面PAE D. 平面PDE⊥平面ABC
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线的中心在原点，焦点为
，
且离心率
.
（1）求双曲线的方程；
（2）求以点
为中点的弦所在的直线方程.
【答案】（1）
；（2）
.
【解析】
（1）根据焦点坐标求得
,根据离心率及
求得
的值，进而求得双曲线的标准方程.（2）设出
两点的坐标，利用点差法求得弦所在直线的斜率，再由点斜式求得弦所在的直线方程.
（1） 由题可得
，
，∴
，
,
所以双曲线方程 
.
（2）设弦的两端点分别为
，
，
则由点差法有：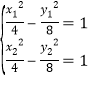
, 上下式相减有：
又因为
为中点，所以
，
,
∴
，所以由直线的点斜式可得
,
即直线的方程为
.
经检验满足题意.
【点睛】
本小题主要考查双曲线标准方程的求法，考查利用点差法求解有关弦的中点有关的问题，属于中档题
【题型】解答题
【结束】
19
【题目】某投资公司计划投资
，
两种金融产品，根据市场调查与预测，产品的利润
与投资金额
的函数关系为
，产品的利润
与投资金额的函数关系为
.（注：利润与投资金额单位：万元）
（1）该公司已有100万元资金，并全部投入，两种产品中，其中万元资金投入产品，试把，两种产品利润总和表示为的函数，并写出定义域；
（2）试问：怎样分配这100万元资金，才能使公司获得最大利润？其最大利润为多少万元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
