Question

20．如图1，有一建筑物OP，为了测量它的高度，在地面上选一基线AB，设其长度为d，在A点处测得P点的仰角为α，在B点处测得P点的仰角为β．
（1）若AB=40，α=30°，β=45°，且∠AOB=30°，求建筑物的高度h；
（2）经分析若干测得的数据后，发现将基线AB调整到线段AO上（如图2），α与β之差尽量大时，可以
提高测量精确度，设调整后AB的距离为d，tanβ=$\frac{4}{d}$，建筑物的实际高度为21，试问d为何值时，β-α最大？

Answer 1

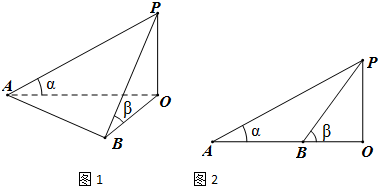
分析 （1）利用余弦定理，可得AB²=OA²+OB²-2OA•OBcos∠AOB，即可求旗杆的高度h；
（2）计算tan（β-α），利用基本不等式，结合正切函数的单调性，即可得到结论．

解答 解：（1）在Rt△POA中，OA=$\sqrt{3}$h，在Rt△POB中，OB=h，
在Rt△AOB中，d²=（$\sqrt{3}$h）²+h²-2•$\sqrt{3}$h•hcos30°，其中：d=40，得：h=40，
故旗杆的高度为40．
（2）∵tanα=$\frac{h}{d+\frac{dh}{4}}$，tanβ=$\frac{4}{d}$，
∴tan（β-α）=$\frac{\frac{4}{d}-\frac{4h}{d（h+4）}}{1+\frac{16h}{{d}^{2}（h+4）}}$=$\frac{16d}{{d}^{2}（h+4）+16h}$=$\frac{16}{d（h+4）+\frac{16h}{d}}$≤$\frac{16}{2\sqrt{16h（h+4）}}$=$\frac{2}{\sqrt{h（h+4）}}$=$\frac{2\sqrt{21}}{105}$，
当且仅当d（h+4）=$\frac{16h}{d}$即d=$\frac{4\sqrt{21}}{5}$时“=”成立，
故当d=$\frac{4\sqrt{21}}{5}$时，tan（β-α）最大，
∵0＜α＜β＜$\frac{π}{2}$，∴0＜β-α＜$\frac{π}{2}$，
∴当d=$\frac{4\sqrt{21}}{5}$时，β-α最大．

点评 本题考查余弦定理的运用，考查差角的正切公式，考查正切函数的单调性，考查了转化思想和数形结合思想的应用，属于中档题．