
分析 设AC=40,BC=60.利用截距式可得直线AB的方程为$\frac{x}{40}+\frac{y}{60}=1$,S矩形CDEF=xy,利用基本不等式求解xy的最大值即可.
解答 解:如图所示: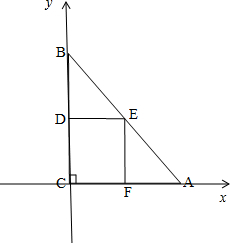
设AC=40,BC=60.
则直线AB的方程为$\frac{x}{40}+\frac{y}{60}=1$
设E(x,y),则$\frac{x}{40}+\frac{y}{60}=1$(0<x<40,0<y<60),
故有1≥2$\sqrt{\frac{x}{40}•\frac{y}{60}}$,化为:xy≤600,当且仅当$\frac{x}{40}=\frac{y}{60}=\frac{1}{2}$,即x=20,y=30时取等号.
∴S矩形CDEF=xy≤600.
∵△ABC的面积S$\frac{1}{2}$×40×60=1200.是固定的,
∴当使得DE=20,EF=30,剪下矩形CDEF的面积最大时,才能使剩下的残料最少.
故答案为:600.
点评 本题考查了基本不等式的应用、直线的截距式等基础知识与基本方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com