
���� ���ݶ���ֱ����f��x��=0��g��x��=0������������ת��Ϊsin2[x]+sin2{x}-1=0��[x]•{x}=$\frac{x}{3}$+1���ֱ�����ͼ�����������������ĸ�����
��� �⣺��f��x��=sin2[x]+sin2{x}-1=0��sin2{x}=1-sin2[x]=cos2[x]��
��{x}=$\frac{��}{2}$+2k��+[x]��{x}=-$\frac{��}{2}$+2k��+[x]��
��{x}-[x]=$\frac{��}{2}$+2k�л�{x}-[x]=-$\frac{��}{2}$+2k�У�
��x=$\frac{��}{2}$+2k�л�x=-$\frac{��}{2}$+2k�У�
��x=$\frac{��}{2}$+2k����0��x��100��
�൱k=0ʱ��x=$\frac{��}{2}$����x=$\frac{��}{2}$+2k�С�100�����k��15.68����k��15����ʱ��15����㣬
��x=-$\frac{��}{2}$+2k����0��x��100��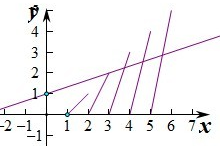
�൱k=0ʱ��x=-$\frac{��}{2}$����������x=-$\frac{��}{2}$+2k�С�100�����k��16.28����ʱ��15����㣬
����f��x��=sin2[x]+sin2{x}-1��������Ϊ15+15=30����
��{x}=$\left\{\begin{array}{l}{x��0��x��1}\\{x-1��1��x��2}\\{x-2.2��x��3}\\{��}\\{x-99��99��x��100}\\{x-100��x=100}\end{array}\right.$��
��[x]•{x}=$\left\{\begin{array}{l}{0��0��x��1\\;}\\{x-1��1��x��1}\\{2��x-2����2��x��3}\\{��}\\{99��x-99����99��x��100}\\{100��x-100����x=100}\end{array}\right.$����g��x��=0��[x]•{x}=$\frac{x}{3}$+1���ֱ���������h��x��=[x]{x}��y=$\frac{x}{3}$+1��ͼ����ͼ��
��ͼ���֪��0��x��1��1��x��2ʱ������h��x��=[x]{x}��y=$\frac{x}{3}$+1û�н��㣬
��2��x��3ʱ������h��x��=[x]{x}��y=$\frac{x}{3}$+1��ÿһ��������ֻ��һ�����㣬
��0��x��100��
��g��x��=[x]•{x}-$\frac{x}{3}$-1��������Ϊ100-2-1=97����
��m=30��n=97��
m+n=127��
�ʴ�Ϊ��127��
���� ������Ҫ���麯�����¶����⣬���ö�������������ͼ���������ν���ǽ������Ĺؼ����ۺ��Խ�ǿ���ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-1 | B�� | a��-1 | C�� | a��2 | D�� | -1��a��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $y={��\frac{1}{2}��^x}$ | B�� | $y=\frac{2}{x}$ | C�� | y=-2x3 | D�� | $y=-\frac{1}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com