
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
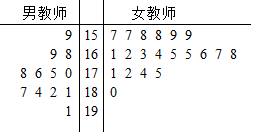 新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.
新疆某中学共有教师32人,其中男教师12人,女教师20人,这32名教师的身高如下面的茎叶图所示(单位:cm).为“打击疆独分子,确保学校师生安全”,校委会决定:身高在175cm以上(含175cm)的男教师和身高在172cm以上(含172cm)的女教师组成“校外巡逻队”,其余教师组成“校内巡逻队”.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com