
【题目】已知圆![]() ,一动圆
,一动圆![]() 与直线
与直线![]() 相切且与圆
相切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() ,交(1)中轨迹
,交(1)中轨迹![]() 于
于![]() 两点,若
两点,若![]() 中点的纵坐标为
中点的纵坐标为![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用直接法,求动圆圆心P的轨迹T的方程;
(2)法一:由(1)得抛物线E的焦点C(1,0)设A,B两点的坐标分别为A(x1,y1),B(x2,y2),利用点差法,求出线段AB中点的纵坐标,得到直线的斜率,求出直线方程.
法二:设直线l的方程为x=my+1,联立直线与抛物线方程,设A,B两点的坐标分别为A(x1,y1),B(x2,y2),通过韦达定理,求出m即可.
(1)设P(x,y),则由题意,|PC|﹣(x![]() )
)![]() ,
,
∴![]() x+1,
x+1,
化简可得动圆圆心P的轨迹E的方程为y2=4x;
(2)法一:由(1)得抛物线E的方程为y2=4x,焦点C(1,0)
设A,B两点的坐标分别为A(x1,y1),B(x2,y2),
则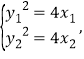
两式相减.整理得![]()
∵线段AB中点的纵坐标为﹣1
∴直线l的斜率![]()
直线l的方程为y﹣0=﹣2(x﹣1)即2x+y﹣2=0.
法二:由(1)得抛物线E的方程为y2=4x,焦点C(1,0)
设直线l的方程为x=my+1
由![]() 消去x,得y2﹣4my﹣4=0
消去x,得y2﹣4my﹣4=0
设A,B两点的坐标分别为A(x1,y1),B(x2,y2),
∵线段AB中点的纵坐标为﹣1
∴![]()
解得![]()
直线l的方程为![]() 即2x+y﹣2=0.
即2x+y﹣2=0.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务蓬勃发展,有关部门推出了针对网购平台的商品和服务的评价系统,从该系统中随机选出100名交易者,并对其交易评价进行了统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的有40人.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对服务满意与对商品满意之间有关”?
的把握认为“网购者对服务满意与对商品满意之间有关”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)若对商品和服务都不满意者的集合为![]() .已知
.已知![]() 中有2名男性,现从
中有2名男性,现从![]() 中任取2人调查其意见.求取到的2人恰好是一男一女的概率.
中任取2人调查其意见.求取到的2人恰好是一男一女的概率.
附: 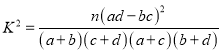 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)求直线![]() 所过定点
所过定点![]() 的坐标;
的坐标;
(2)求直线![]() 被圆
被圆![]() 所截得的弦长最短时
所截得的弦长最短时![]() 的值;
的值;
(3)已知点![]() ,在直线
,在直线![]() (
(![]() 为圆心)上存在定点
为圆心)上存在定点![]() (异于点
(异于点![]() ),满足:对于圆
),满足:对于圆![]() 上任一点
上任一点![]() ,都有
,都有![]() 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点![]() 的坐标及该常数.
的坐标及该常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com