Question

【题目】已知函数．

（1）当时，试求在处的切线方程；

（2）当时，试求的单调区间；

（3）若在内有极值，试求的取值范围．

Answer 1

【答案】（1）；（2）单调增区间为，单调减区间为；（3）．

【解析】

试题分析：（1）求导，利用导数的几何意义求解；（2）求导，研究导函数的取值情况即可求解；（3）问题等价于有解，求导后分析其取值情况即可．

试题解析：（1）当时，，，．方程为；（2）0，当时，对于，恒成立，所以，；，，所以单调增区间为，单调减区间为；（3）若在内有极值，则在内有解，令，，，设，，所以， 当时，恒成立，所以单调递减，又因为，又当时，，即在上的值域为，

所以当时， 有解．

设，则，，所以在单调递减，

因为，，

所以在有唯一解，

所以有：

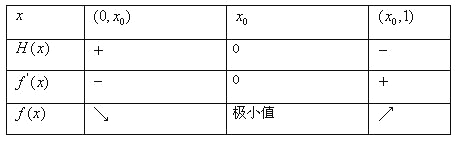
所以当时，在内有极值且唯一，当时，当时，恒成立，单调递增，不成立，综上，的取值范围为．