
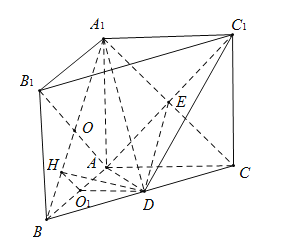
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 中点.
中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)由等腰三角形和直棱柱的性质,得出![]() 和
和![]() ,根据线面垂直的判定定理,即可证出
,根据线面垂直的判定定理,即可证出![]() 平面
平面![]() ;
;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,结合三角形的中位线得出
,结合三角形的中位线得出![]() ,根据线面平行的判定定理,即可证出
,根据线面平行的判定定理,即可证出![]() 平面
平面![]() ;
;
(3)连![]() ,交
,交![]() 于点
于点![]() ,分别取
,分别取![]() 、
、![]() 中点
中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,根据线面垂直的判定定理,可证出
,根据线面垂直的判定定理,可证出![]() 平面
平面![]() 和
和![]() 平面
平面![]() ,从而得出
,从而得出![]() 就是二面角
就是二面角![]() 的平面角,最后利用几何法求出二面角
的平面角,最后利用几何法求出二面角![]() 的余弦值.
的余弦值.
解:(1)证明:![]() ,
,![]() 是
是![]() 中点,
中点,![]() ,
,
又![]() 在直三棱柱
在直三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)证明:连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
![]() 是
是![]() 的中位线,
的中位线,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
(3)解:连![]() ,交
,交![]() 于点
于点![]() ,分别取
,分别取![]() 、
、![]() 中点
中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,
![]() 四边形
四边形![]() 是正方形且
是正方形且![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,故
的中点,故![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点且
中点且![]() ,
,
![]() ,
,
又![]() 在直三棱柱
在直三棱柱![]() 中,
中,![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
又![]() 平面
平面![]() 平面
平面![]()
![]() 就是二面角
就是二面角![]() 的平面角,
的平面角,
设![]() ,则在
,则在![]() 中,
中,![]() ,
,
![]() ,
,
故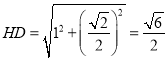 ,
,
故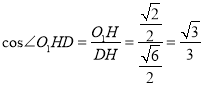 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
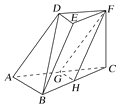
(1)求证:BD∥平面FGH;
(2)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45° ,求平面FGH与平面ACFD所成的角(锐角)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() g(x)=f(x)+
g(x)=f(x)+![]() x-6lnx,其中
x-6lnx,其中![]() R.
R.
(1)当![]() =1时,判断f(x)的单调性;
=1时,判断f(x)的单调性;
(2)当![]() =2时,求出g(x)在(0,1)上的最大值;
=2时,求出g(x)在(0,1)上的最大值;
(3)设函数![]() 当
当![]() =2时,若
=2时,若![]() 总有
总有![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,下列结论错误的是( )
A. 月接待游客量逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,
,![]() ,②
,②![]() ,
,![]() ,③
,③![]() ,
,![]() 三个条件中任选一个补充在下面问题中,并加以解答.
三个条件中任选一个补充在下面问题中,并加以解答.
已知![]() 的内角A,B,C的对边分别为a,b,c,若
的内角A,B,C的对边分别为a,b,c,若![]() ,______,求
,______,求![]() 的面积S.
的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com