
分析 (1)直线l1的极坐标方程为ρsinθ+ρcosθ=1,利用互化公式化为直角坐标方程.直线l2的极坐标方程为θ=$\frac{π}{3}$(ρ=R),利用互化公式可得直角坐标方程.
(2)把θ=$\frac{π}{3}$(ρ=R),代入直线l1的极坐标方程为ρsin$\frac{π}{3}$+ρcos$\frac{π}{3}$=1,化简可得ρ.即可得出两直线l1与l2交点的极坐标.
解答 解:(1)直线l1的极坐标方程为ρsinθ+ρcosθ=1,化为:直角坐标方程:y+x-1=0.
直线l2的极坐标方程为θ=$\frac{π}{3}$(ρ=R),可得直角坐标方程:y=$\sqrt{3}$x,即$\sqrt{3}$x-y=0.
(2)把θ=$\frac{π}{3}$(ρ=R),代入直线l1的极坐标方程为ρsin$\frac{π}{3}$+ρcos$\frac{π}{3}$=1,化为$ρ=\sqrt{3}$-1.
∴两直线l1与l2交点的极坐标为:$(\sqrt{3}-1,\frac{π}{3})$.
点评 本题考查了极坐标方程化为直角坐标方程、极坐标方程的应用、直线的交点,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-3,+∞) | C. | (-∞,0) | D. | (-∞,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
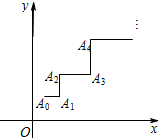 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
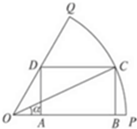 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,记∠COP=α,矩形的面积为S;
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,记∠COP=α,矩形的面积为S;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com