
| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{13}{2}$ |
分析 ${a_n}+{a_{n+1}}=\frac{1}{2}({n∈{N^*}})$,a2=2,可得a1+2=$\frac{1}{2}$,解得a1.a2n+a2n+1=$\frac{1}{2}$,即可得出.
解答 解:∵${a_n}+{a_{n+1}}=\frac{1}{2}({n∈{N^*}})$,a2=2,∴a1+2=$\frac{1}{2}$,解得a1=-$\frac{3}{2}$.
∴a2n+a2n+1=$\frac{1}{2}$,
∴S21=-$\frac{3}{2}$+$\frac{1}{2}×$10=$\frac{7}{2}$.
故选:B.
点评 本题考查了数列递推关系、分组求和方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 理科 | 文科 | 合计 | |
| 男 | 30 | ||
| 女 | 35 | 45 | |
| 合计 | 60 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| K0 | 0.445 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
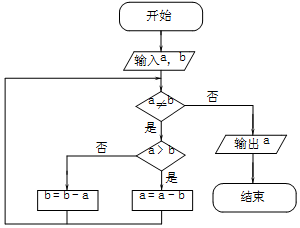 更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是( )
更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是( )| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cb2<ab2 | B. | ab<ac | C. | c(a-c)>0 | D. | a+ac>b+ac |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com