Question

16．已知定义在[1，+∞）上的函数f（x）=$\left\{\begin{array}{l}{-8x（x-2），1≤x＜2}\\{\frac{1}{2}f（\frac{x}{2}），x≥2}\end{array}\right.$给出下列结论：
①函数f（x）的值域为（0，8]；
②对任意的n∈N，都有f（2ⁿ）=2^3-n；
③存在k∈（$\frac{1}{8}$，$\frac{1}{4}$），使得直线y=kx与函数y=f（x）的图象有5个公共点；
④“函数f（x）在区间（a，b）上单调递减”的充要条件是“存在n∈N，使得（a，b）⊆（2ⁿ，2ⁿ⁺¹）”
其中正确命题的序号是（　　）

• A． ①②③
• B． ①③④
• C． ①②④
• D． ②③④

Answer 1

分析 ①根据分段函数的表达式结合函数的最值进行求解判断，
②利用f（2ⁿ）=$\frac{1}{{2}^{n}}$f（1）进行求解判断，
③作出函数f（x）和y=kx的图象，利用数形结合进行判断，
④根据分段函数的单调性进行判断．

解答 解：①当1≤x＜2时，f（x）=-8x（x-2）=-8（x-1）²+8∈（0，8]，
②∵f（1）=8，
∴f（2ⁿ）=$\frac{1}{2}$f（2^n-1）=$\frac{1}{{2}^{2}}$f（2^n-2）=$\frac{1}{{2}^{3}}$f（2^n-3）=…=$\frac{1}{{2}^{n}}$f（2⁰）=$\frac{1}{{2}^{n}}$f（1）=$\frac{1}{{2}^{n}}$×8=2^3-n，故②正确，
③当x≥2时，f（x）=$\frac{1}{2}$f（$\frac{x}{2}$）∈0，4]，故函数f（x）的值域为（0，8]；故①正确，
当2≤x＜4时，1≤$\frac{x}{2}$＜2，则f（x）=$\frac{1}{2}$f（$\frac{x}{2}$）=$\frac{1}{2}$[-8（$\frac{x}{2}$-1）²+8]=-4（$\frac{x}{2}$-1）²+4，
当4≤x＜8时，2≤$\frac{x}{2}$＜4，则f（x）=$\frac{1}{2}$f（$\frac{x}{2}$）=$\frac{1}{2}$[-4（$\frac{x}{4}$-1）²+4]=-2（$\frac{x}{4}$-1）²+2
作出函数f（x）的图象如图：
作出y=$\frac{1}{4}$x和y=$\frac{1}{8}$x的图象如图，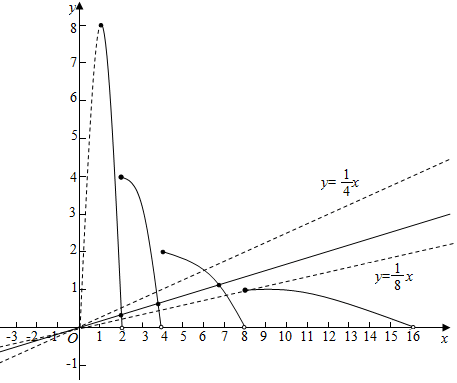

当k∈（$\frac{1}{8}$，$\frac{1}{4}$），使得直线y=kx与函数y=f（x）的图象有3个公共点；故③错误，
④由分段函数的表达式得当x∈（2ⁿ，2ⁿ⁺¹）时，函数f（x）在（2ⁿ，2ⁿ⁺¹）上为单调递减函数，
则函数f（x）在区间（a，b）上单调递减”的充要条件是“存在n∈N，使得（a，b）⊆（2ⁿ，2ⁿ⁺¹）”为真命题．，故④正确，
故选：C

点评 本题主要考查命题的真假判断，涉及分段函数的图象和性质，作出函数的图象以及利用函数递推关系是解决本题的关键．综合性较强，难度较大．