
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“?x∈R,使x2+x+1<0”的否定为:“?x∈R,使x2+x+1<0” | |
| C. | 命题“若f(x)=$\frac{1}{3}$x3-2x2+4x+2,则2是函数f(x)的极值点”为真命题 | |
| D. | 命题“若抛物线的方程为y=-4x2,则焦点到其准线的距离为$\frac{1}{8}$”的逆否命题为真命题 |
分析 对4个命题分别进行判断,即可得出结论.
解答 解:对于A,命题“若x2=1,则x=1”的否命题为:“若x2≠1,则x≠1”,不正确;
对于B,命题“?x∈R,使x2+x+1<0”的否定为:“?x∈R,使x2+x+1≥0”,不正确;
对于C,f(x)=$\frac{1}{3}$x3-2x2+4x+2,则f′(x)=x2-4x+4=(x-2)2,∴函数在2的左右附近,导数的符号不改变,∴命题“若f(x)=$\frac{1}{3}$x3-2x2+4x+2,则2是函数f(x)的极值点”为假命题;
对于D,若抛物线的方程为y=-4x2,则焦点到其准线的距离为$\frac{1}{8}$,正确,根据原命题与逆否命题是等价命题,故命题“若抛物线的方程为y=-4x2,则焦点到其准线的距离为$\frac{1}{8}$”的逆否命题为真命题,正确.
故选:D.
点评 本题考查否命题、命题的否定、逆否命题,考查函数的极值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
 如图,一个用斜二测法画出的水平放置的平面直观图,是一个直角梯形,O′A=5,AB=2,BD=3,∠O′AB=∠ABD=90°,则它的实际图形和面积分别是( )
如图,一个用斜二测法画出的水平放置的平面直观图,是一个直角梯形,O′A=5,AB=2,BD=3,∠O′AB=∠ABD=90°,则它的实际图形和面积分别是( )| A. | 直角梯形、面积是16$\sqrt{2}$ | B. | 直角梯形、面积是8 | ||
| C. | 梯形非直角,面积是16 | D. | 梯形非直角,面积是8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | :?x≥-1,x2≤1 | B. | ?x<-1,x2≤1 | C. | :?x<-1,x2≤1 | D. | ?x≥-1,x2≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
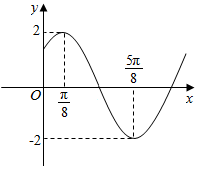 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )| A. | 函数g(x)的奇函数 | |
| B. | 函数f(x)与g(x)的图象均关于直线x=-$\frac{15}{8}$π对称 | |
| C. | 函数f(x)与g(x)的图象均关于点(-$\frac{π}{4}$,0)对称 | |
| D. | 函数f(x)与g(x)在区间(-$\frac{π}{3}$,0)上均单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | -1 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com