
分析 (1)分别记“甲、乙、丙三位同学通过笔试”为事件A,B,C,事件E表示“甲、乙、丙三位同学恰有两位通过笔试”,利用对立事件概率计算公式、互斥事件概率加法公式、相互独立事件概率乘法公式能求出甲、乙、丙三位同学恰有两位通过笔试的概率.
(2)“甲乙丙三位同学各自经过两次考试后能被录取”分别记为事件D,E,F,由题意X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望E(X).
解答 解:(1)分别记“甲、乙、丙三位同学通过笔试”为事件A,B,C,
事件E表示“甲、乙、丙三位同学恰有两位通过笔试”,
则甲、乙、丙三位同学恰有两位通过笔试的概率:
P(E)=P(AB$\overline{C}$)+P(A$\overline{B}$C)+P($\overline{A}$BC)
=$\frac{1}{3}×\frac{1}{2}×\frac{4}{5}$+$\frac{1}{3}×\frac{1}{2}×\frac{1}{5}$+$\frac{2}{3}×\frac{1}{2}×\frac{1}{5}$
=$\frac{7}{30}$.
(2)“甲乙丙三位同学各自经过两次考试后能被录取”分别记为事件D,E,F,
则P(D)=$\frac{1}{3}×\frac{1}{5}$=$\frac{1}{15}$,P(E)=$\frac{1}{2}×\frac{1}{4}$=$\frac{1}{8}$,P(F)=$\frac{1}{5}×\frac{1}{2}$=$\frac{1}{10}$,
由题意X的可能取值为0,1,2,3,
P(X=0)=P($\overline{D}\overline{E}\overline{F}$)=$\frac{14}{15}×\frac{7}{8}×\frac{9}{10}$=$\frac{882}{1200}$,
P(X=1)=P($D\overline{E}\overline{F}$+$\overline{D}E\overline{F}$+$\overline{D}\overline{E}F$)=$\frac{1}{15}×\frac{7}{8}×\frac{9}{10}$+$\frac{14}{15}×\frac{1}{8}×\frac{9}{10}$+$\frac{14}{15}×\frac{7}{8}×\frac{1}{10}$=$\frac{287}{1200}$,
P(X=2)=P($DE\overline{F}$+D$\overline{E}F$+$\overline{D}EF$)=$\frac{1}{15}×\frac{1}{8}×\frac{9}{10}+\frac{1}{15}×\frac{7}{8}×\frac{1}{10}+\frac{14}{15}×\frac{1}{8}×\frac{1}{10}$=$\frac{30}{1200}$,
P(X=3)=P(DEF)=$\frac{1}{15}×\frac{1}{8}×\frac{1}{10}$=$\frac{1}{1200}$,
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{882}{1200}$ | $\frac{287}{1200}$ | $\frac{30}{1200}$ | $\frac{1}{1200}$ |
点评 本题考查概率的求法,考查离散型随机变量数学期望的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式、互斥事件概率加法公式、相互独立事件概率乘法公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 命题“?x∈R,使x2+x+1<0”的否定为:“?x∈R,使x2+x+1<0” | |
| C. | 命题“若f(x)=$\frac{1}{3}$x3-2x2+4x+2,则2是函数f(x)的极值点”为真命题 | |
| D. | 命题“若抛物线的方程为y=-4x2,则焦点到其准线的距离为$\frac{1}{8}$”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x(月份) | 1 | 2 | 3 | 4 | 5 |
| y(万盒) | 4 | 4 | 5 | 6 | 6 |
| A. | 6.8万盒 | B. | 7.0万盒 | C. | 7.2万盒 | D. | 7.4万盒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
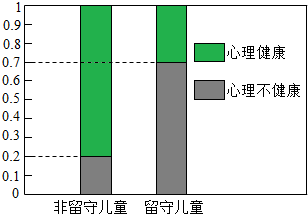
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
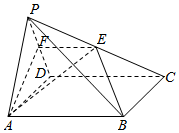 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com