
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
分析 (1)先求出年份代号t和人均纯收入y的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程;
(2)由(1)知,b=0.5>0,2009年至2015年该地区居民家庭人均纯收入逐年增加,平均每年增加0.5千元,求得2017年的年份代号t=9代入(1)的回归方程,得y的值.
解答 解:(1)由所给数据计算得
$\overline{t}$=$\frac{1+2+3+4+5+6+7}{7}$=4,
$\overline{y}$=$\frac{2.9+3.3+3.6+4.4+4.8+5.2+5.9}{7}$=4.4,
$\sum_{i=1}^{7}$(ti-$\overline{t}$)2=9+4+1+0+1+4+9=28,
$\sum_{i=1}^{7}$(ti-$\overline{t}$)(yi-$\overline{y}$)=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+1×0.5+2×0.9+3×1.6=14.,…4分
$\widehatb=\frac{{\sum_{i=1}^n{({t_i}-\overline t)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({t_i}-\overline t)}^2}}}}$=$\frac{14}{28}$=0.5,$\widehata=\overline y-\widehatb\overline t$=4.3-0.5×4=2.3,
所求回归方程为y=0.5t+2.3…8分
(2)由(1)知,b=0.5>0,故2009年至2015年该地区居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2017年的年份代号t=9代入(1)的回归方程,得y=6.8,
故预测该地区2017年该地区居民家庭人均纯收入约为6.8千元.…12分.
点评 本题考查线性回归方程的求法,考查利用线性回归方程进行预测,属于基础题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
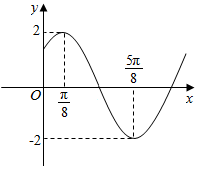 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )| A. | 函数g(x)的奇函数 | |
| B. | 函数f(x)与g(x)的图象均关于直线x=-$\frac{15}{8}$π对称 | |
| C. | 函数f(x)与g(x)的图象均关于点(-$\frac{π}{4}$,0)对称 | |
| D. | 函数f(x)与g(x)在区间(-$\frac{π}{3}$,0)上均单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com