
分析 (1)通过将点P(an,Sn)代入函数f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x中,利用Sn=$\frac{1}{2}$${{a}_{n}}^{2}$+$\frac{1}{2}$an与Sn-1=$\frac{1}{2}$${{a}_{n-1}}^{2}$+$\frac{1}{2}$an-1(n≥2)作差,进而可知数列{an}是首项和公差均为1的等差数列,计算即得结论;
(2)利用错位相减法计算即得结论;
(3)通过(2)知Tn<9,利用作差法可知数列{Tn}是单调递增数列,进而计算可得结论.
解答 解:(1)∵点P(an,Sn)在函数f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x上,
∴Sn=$\frac{1}{2}$${{a}_{n}}^{2}$+$\frac{1}{2}$an,Sn-1=$\frac{1}{2}$${{a}_{n-1}}^{2}$+$\frac{1}{2}$an-1(n≥2),
两式相减,整理得:(an+an-1)(an-an-1-1)=0,
又∵an>0,
∴an=an-1+1,
又∵S1=$\frac{1}{2}$${{a}_{1}}^{2}$+$\frac{1}{2}$a1,即a1=1,
∴数列{an}是首项和公差均为1的等差数列,
∴an=n;
(2)∵b1=1,3bn-2bn-1=0(n≥2,n∈N*),
∴数列{bn}是首项为1、公比为$\frac{2}{3}$的等比数列,
∴${b_n}={b_1}{q^{n-1}}={({\frac{2}{3}})^{n-1}}$,${c_n}={a_n}{b_n}=n•{({\frac{2}{3}})^{n-1}}$,
∴${T_n}=1+2×{({\frac{2}{3}})^1}+3×{({\frac{2}{3}})^2}+4×{({\frac{2}{3}})^3}+…+(n-1)×{({\frac{2}{3}})^{n-2}}+n×{({\frac{2}{3}})^{n-1}}$,
$\frac{2}{3}$Tn=$(\frac{2}{3})^{1}$+2×$(\frac{2}{3})^{2}$+…+n×$(\frac{2}{3})^{n}$,
两式相减,得:$\frac{1}{3}$Tn=1+$(\frac{2}{3})^{1}$+$(\frac{2}{3})^{2}$+…+$(\frac{2}{3})^{n-1}$-n×$(\frac{2}{3})^{n}$
=$\frac{1-(\frac{2}{3})^{n}}{1-\frac{2}{3}}$-n×$(\frac{2}{3})^{n}$
=3-(n+3)×$(\frac{2}{3})^{n}$,
∴Tn=9-(3n+9)×$(\frac{2}{3})^{n}$;
(3)结论:假设存在整数m、M,使得m<Tn<M对任意正整数n恒成立,且M-m=9.
理由如下:
由(2)知:Tn=9-(3n+9)×$(\frac{2}{3})^{n}$<9,
又∵Tn-1=9-[3(n-1)+9]×$(\frac{2}{3})^{n-1}$,
∴Tn-Tn-1=(3n+6)×$(\frac{2}{3})^{n-1}$-(3n+9)×$(\frac{2}{3})^{n}$=n×$(\frac{2}{3})^{n-1}$>0,
∴数列{Tn}是单调递增数列,
∴(Tn)min=T1=9-12×$\frac{2}{3}$=1,
∴1<Tn<9,
∴m=0,M=9,
∴存在整数m、M,使得m<Tn<M对任意正整数n恒成立,且M-m=9.
点评 本题是一道关于数列与不等式的综合题,考查错位相减法,考查数列的单调性,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| x(月份) | 1 | 2 | 3 | 4 | 5 |
| y(万盒) | 4 | 4 | 5 | 6 | 6 |
| A. | 6.8万盒 | B. | 7.0万盒 | C. | 7.2万盒 | D. | 7.4万盒 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
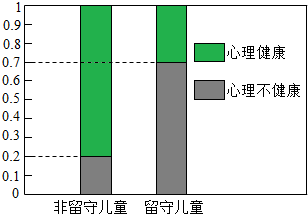
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.015 | B. | 0.005 | C. | 0.985 | D. | 0.995 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
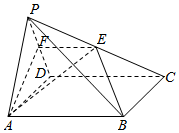 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com