
分析 (Ⅰ)根据函数的解析式计算f(-1)和f(1)的值;
(Ⅱ)根据函数解析式计算f(a)+f(-a)的值;
(Ⅲ)函数f(x)是定义域R上的单调增函数,用单调性的定义即可证明.
解答 解:(Ⅰ)∵$f(x)=\frac{2^x}{{1+{2^x}}}$,
∴f(-1)=$\frac{{2}^{-1}}{1{+2}^{-1}}$=$\frac{1}{3}$,f(1)=$\frac{2}{1+2}$=$\frac{2}{3}$;
(Ⅱ)f(a)+f(-a)=$\frac{{2}^{a}}{1{+2}^{a}}$+$\frac{{2}^{-a}}{1{+2}^{-a}}$=$\frac{{2}^{a}}{1{+2}^{a}}$+$\frac{1}{{2}^{a}+1}$=1;
(Ⅲ)函数f(x)是定义域R上的单调增函数,
证明如下:任取x1、x2∈R,且x1<x2,
∴${2}^{{x}_{1}}$<${2}^{{x}_{2}}$,(1+${2}^{{x}_{1}}$)(1+${2}^{{x}_{2}}$)>0,
∴f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}}{1{+2}^{{x}_{1}}}$-$\frac{{2}^{{x}_{2}}}{1{+2}^{{x}_{2}}}$=$\frac{{2}^{{x}_{1}}{-2}^{{x}_{2}}}{(1{+2}^{{x}_{1}})(1{+2}^{{x}_{2}})}$>0,
即f(x1)<f(x2),
∴函数f(x)是定义域R上的单调增函数.
点评 本题考查了利用函数的解析式求函数值以及利用定义证明函数的单调性问题.是基础题目.


科目:高中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | 丁 | |
| 耐力成绩(X) | 7.5 | m | 8 | 8.5 |
| 体能成绩(Y) | 8 | n | 8.5 | 9.5 |
| 体质成绩(X+Y) | 15.5 | 16 | 16.5 | 18 |
| 体质健康优秀 | 体质健康不优秀 | 总计 | |
| 心肺功能优秀 | 18 | 9 | 27 |
| 心肺功能不优秀 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
| P(K2>k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB中点,F是DC上的点,且$DF=\frac{1}{2}AB,PH$为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB中点,F是DC上的点,且$DF=\frac{1}{2}AB,PH$为△PAD中AD边上的高.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
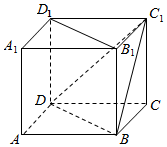 如图,ABCD-A1B1C1D1为正方体.
如图,ABCD-A1B1C1D1为正方体.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | a3>b3 | D. | a2>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com