Question

6．一块边长为6cm的正方形铁皮按如图（1）所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器，将该容器按如图（2）放置，若其正视图为等腰直角三角形（如图（3）），则该容器的体积为（　　）

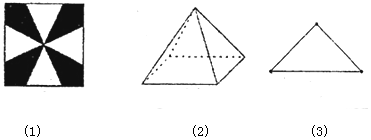
• A． $12\sqrt{6}c{m^3}$
• B． $4\sqrt{6}c{m^3}$
• C． $27\sqrt{2}c{m^3}$
• D． $9\sqrt{2}c{m^3}$

Answer 1

分析 推导出PM+PN=6，且PM=PN，MN=3$\sqrt{2}$，PM=3，设MN中点为O，则PO⊥平面ABCD，由此能求出该容器的体积．

解答 解：如图（2），△PMN是该四棱锥的正视图，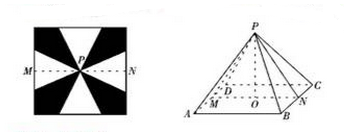
由图（1）知：PM+PN=6，且PM=PN，
由△PMN为等腰直角三角形，知MN=3$\sqrt{2}$，PM=3，
设MN中点为O，则PO⊥平面ABCD，∴PO=$\frac{1}{2}MN=\frac{3\sqrt{2}}{2}$，
∴该容器的体积为${V}_{P-ABCD}=\frac{1}{3}×（3\sqrt{2}）^{2}×\frac{3\sqrt{2}}{2}$=$\frac{1}{3}×18×\frac{3\sqrt{2}}{2}$=9$\sqrt{2}$．
故选：D．

点评 解决本类题目的关键是准确理解几何体的定义，真正把握几何体的结构特征，根据条件构建几何模型，在几何模型中进行判断．